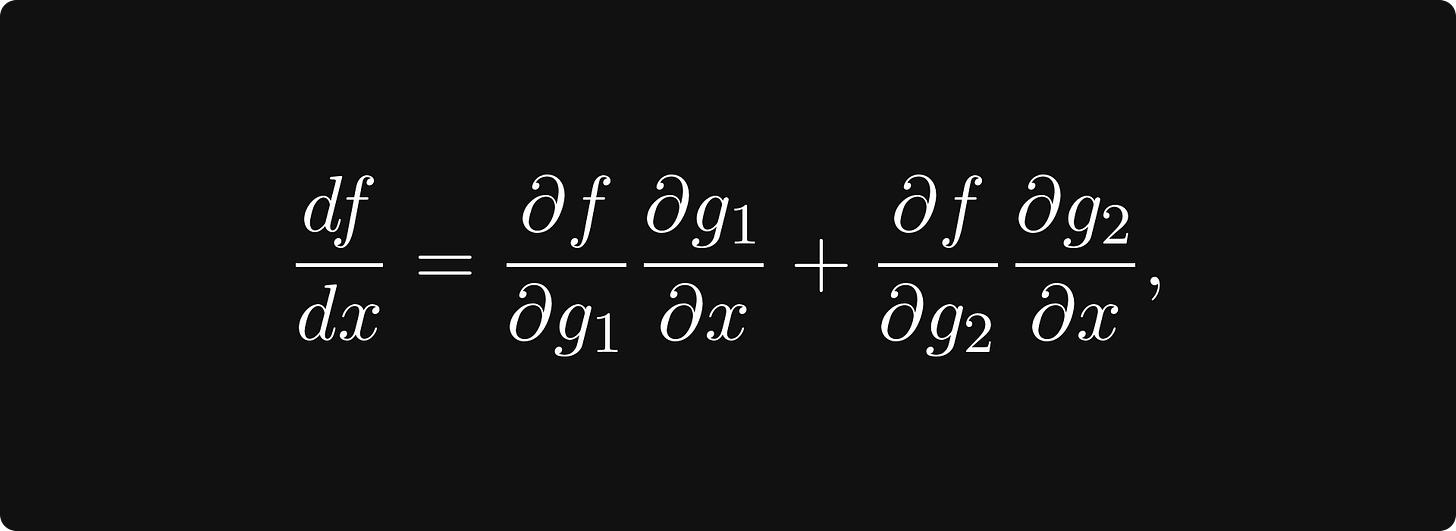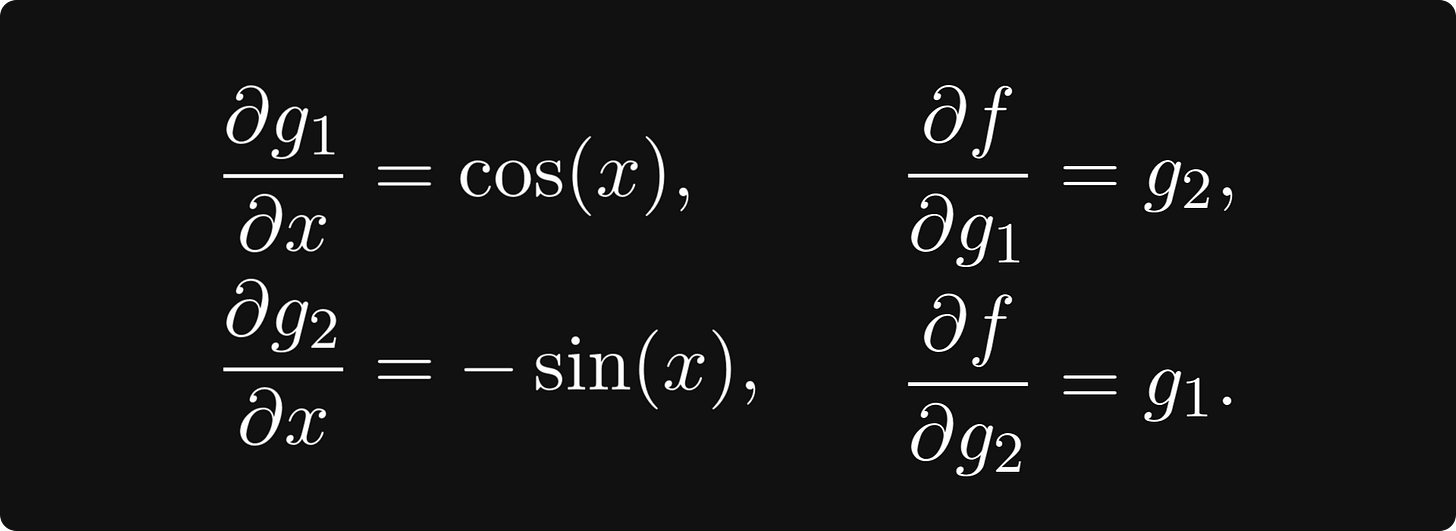Forward vs Backward Differentiation
The algorithm that makes deep learning possible
There are three innovations that make training neural networks with billions of parameters possible.
First, via vectorizing the functions, we can massively parallelize the execution of our algorithms for training and inference.
Second, with gradient descent, we can optimize highly multivariate functions.
Third, with backpropagation, or backwards-mode differentiation, we can efficiently compute the gradient of the loss that we plug directly into gradient descent.
In this episode of the Neural Networks from Scratch series, we’ll see what backwards-mode differentiation exactly is, and why do we need it so much!
This post is the fifth part of my Neural Networks from Scratch series. Although I aim for every post to be self-contained, check out the previous episodes to get you up to speed.
Episode 1: Introduction to Computational Graphs
Episode 2: Computational Graphs as Neural Networks
Episode 3: Computational Graphs and the Forward Pass
Episode 4: The Derivatives of Computational Graphs
Forward-mode differentiation
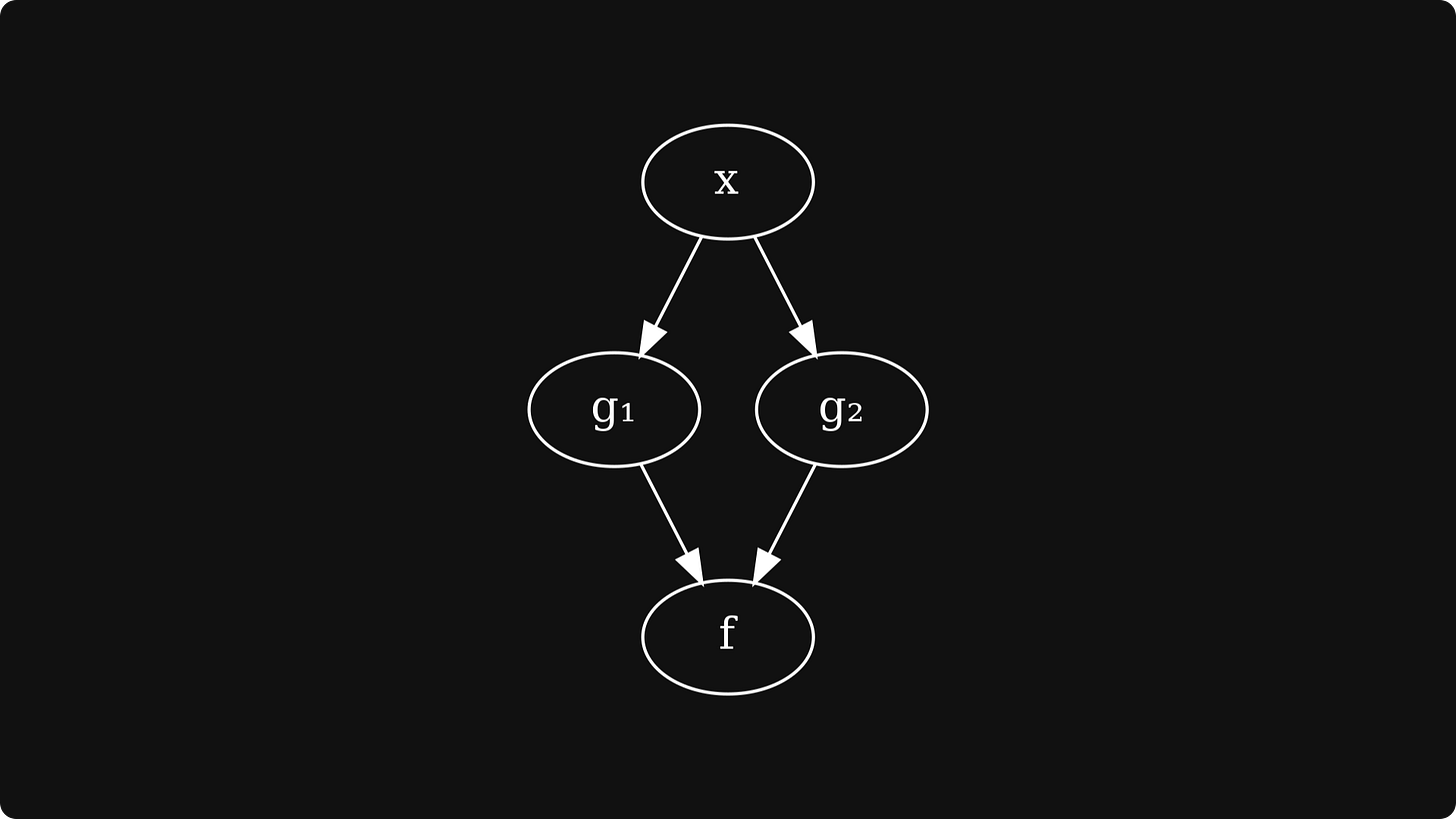
First, let’s recap what forward-mode differentiation is. Consider the expression f(g₁(x),g₂(x)), giving rise to the following computational graph:
To compute df/dx, that is, the derivative of f with respect to x, we apply the chain rule, giving
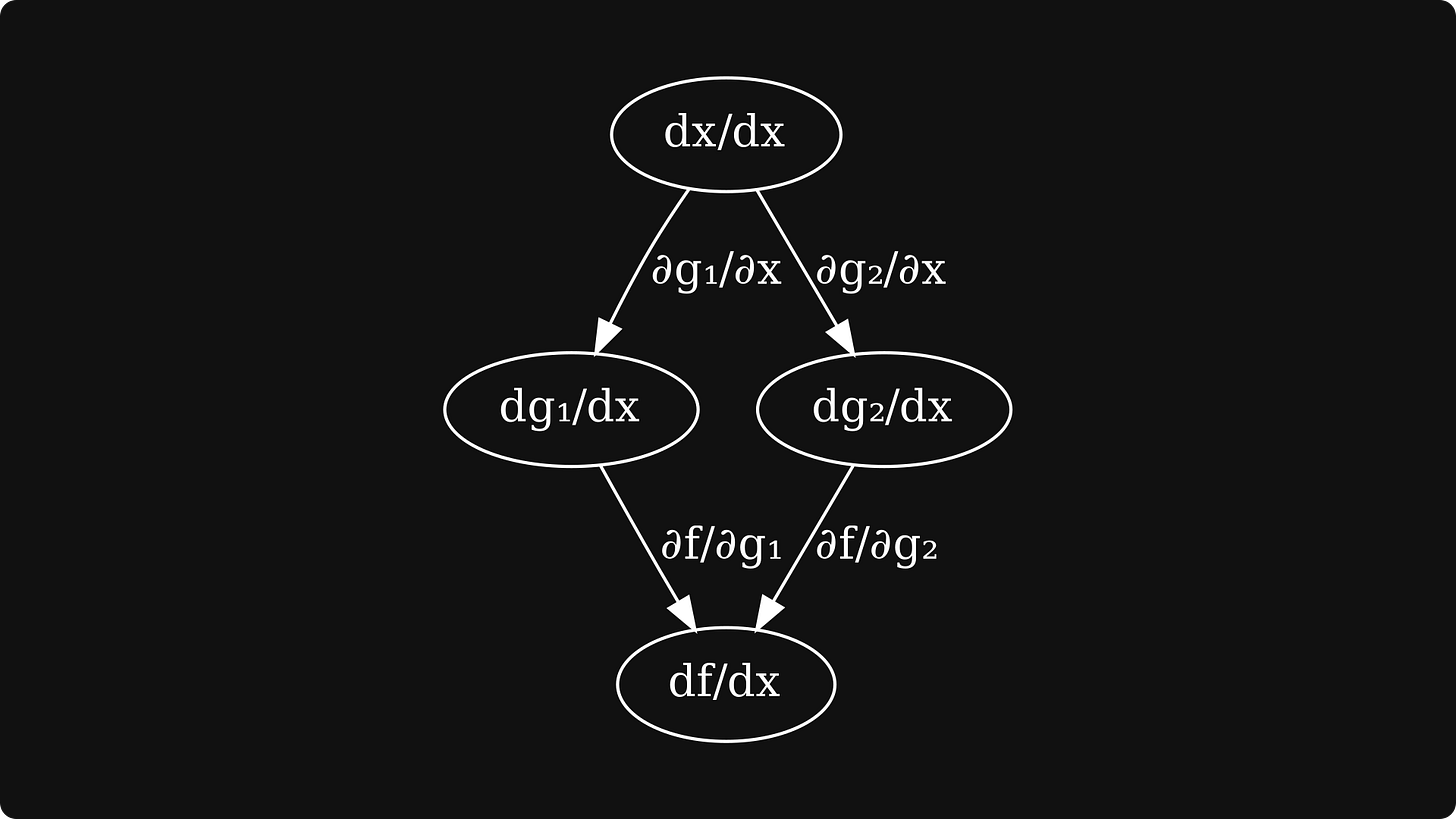
represented by the following computational graph:
In other words, the chain rule tells us that to compute df/dx, we have to
compute the partial derivatives for all edges,
take all paths from the input variable x to the output variable f,
multiply the partial variables along a path,
and sum the product of partial derivatives for all paths.
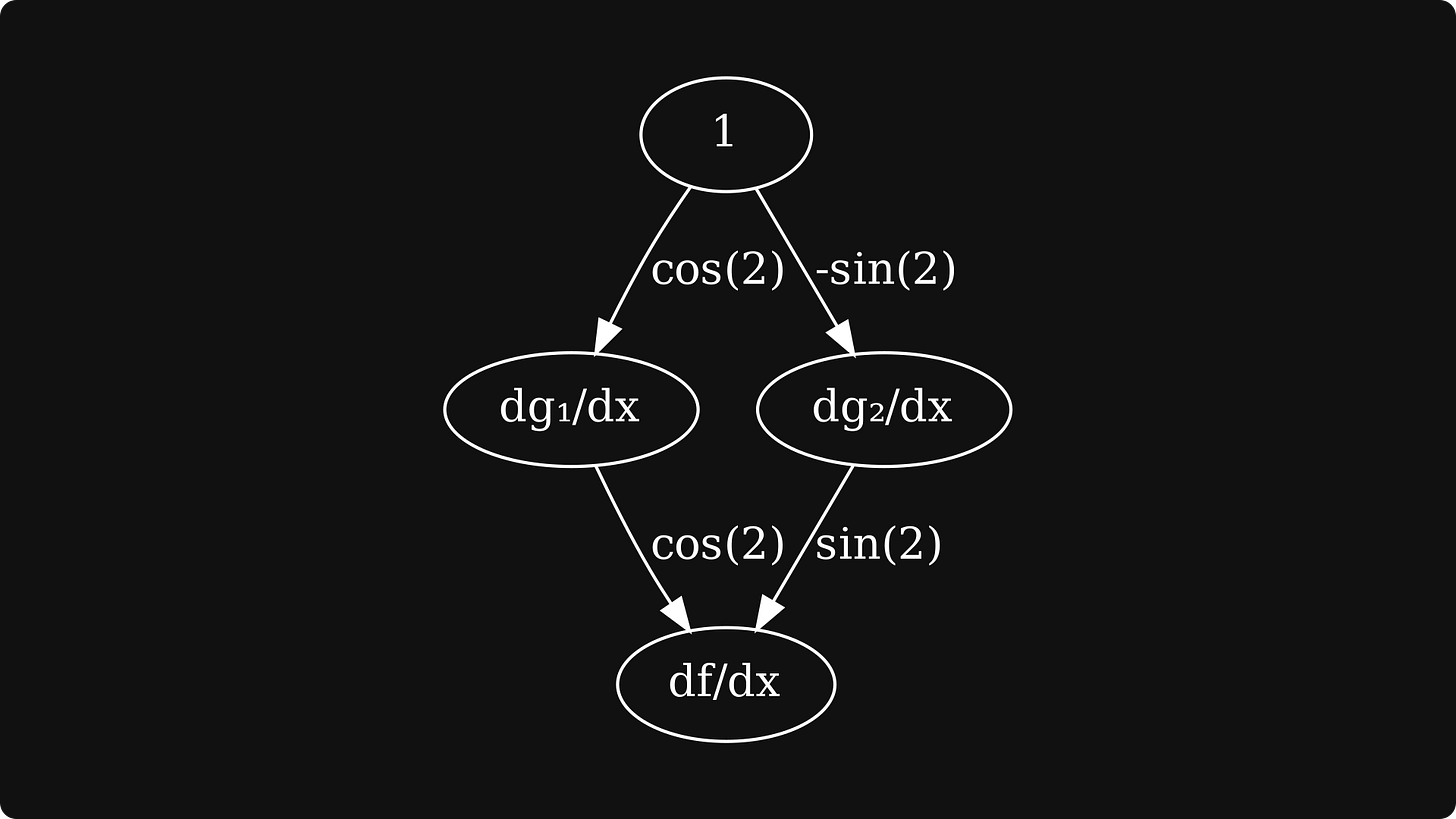
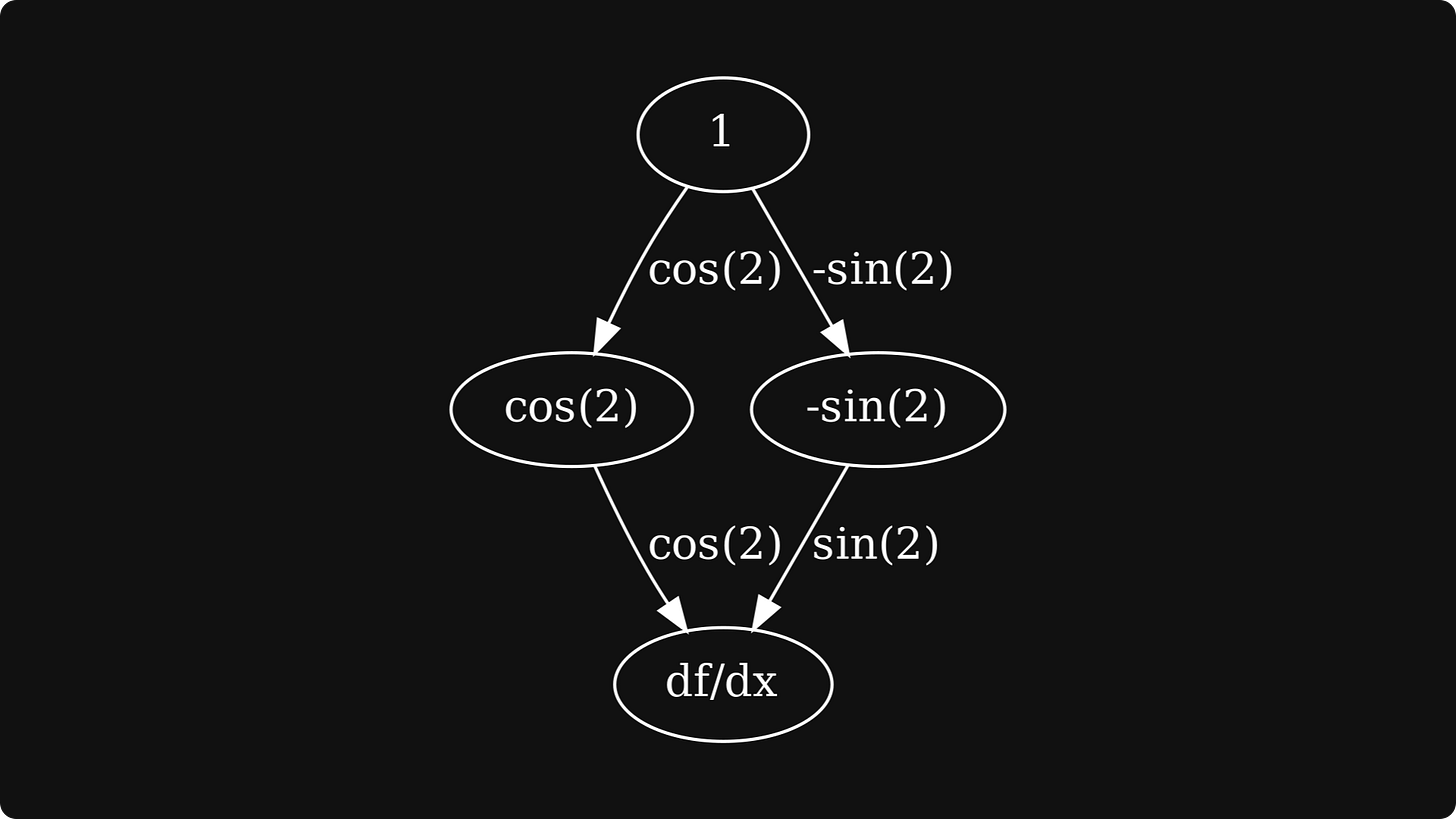
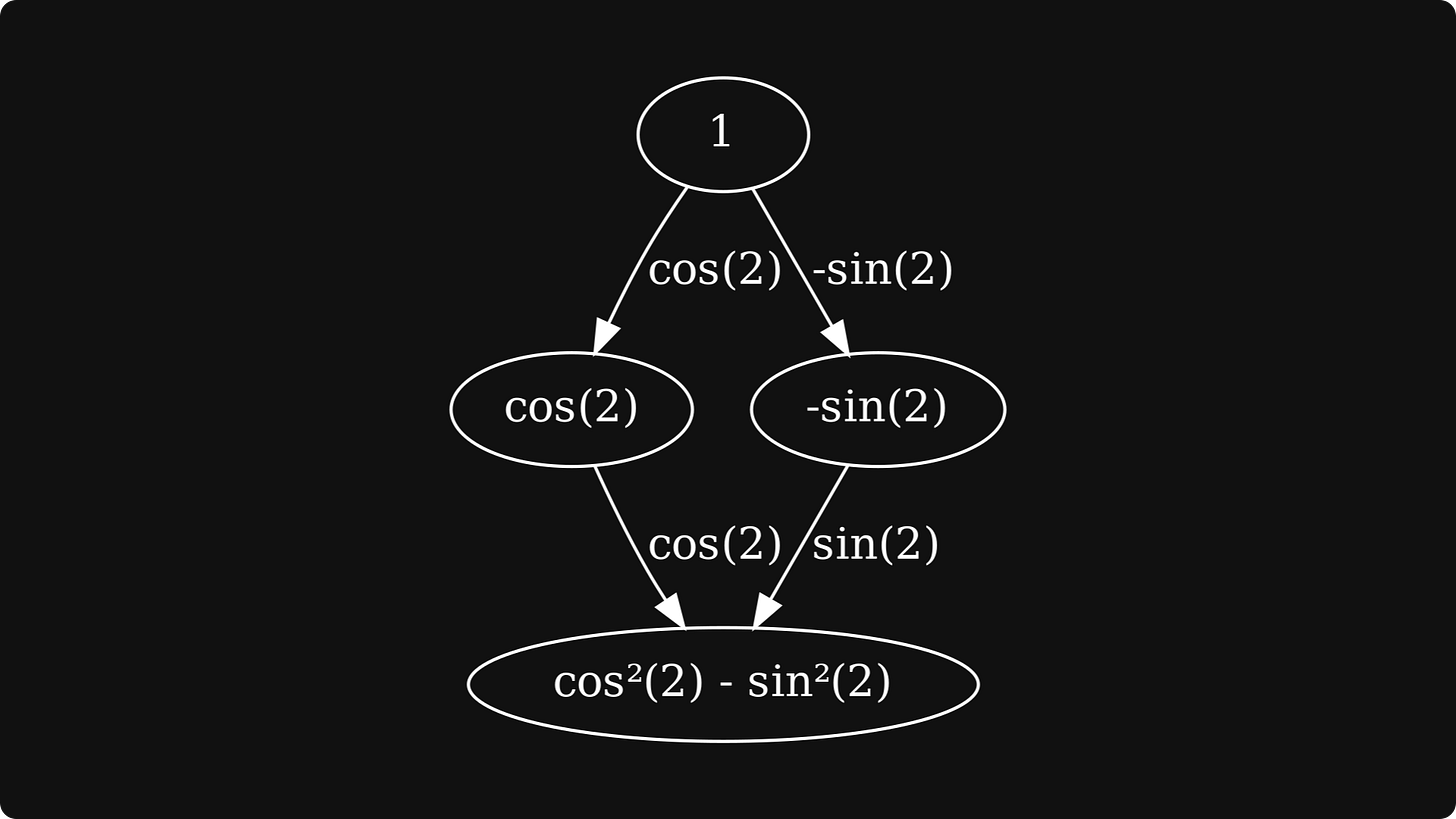
To truly engrave the forward-mode differentiation algorithm into our minds, let’s execute it on a concrete example, say, sin(x) cos(x). This expression is a composition of two univariate functions g₁(x) = sin(x), and g₂(x) = cos(x), and a bivariate function f(g₁, g₂) = g₁ ⋅ g₂.
The partial derivatives are easy to compute:
These form the edges of our derivative graph:
The next step is to compute the derivatives of the first-level nodes, which are simply the partial derivatives in this example.
The final step is to 1) take the derivatives of the first-level nodes, 2) multiply them with the edges coming from dgᵢ/dx to f, 3) and sum them together.
This is the result:
So, what’s the problem with forward differentiation? We’ll see this next.