The Derivatives of Computational Graphs

Part 1. Forward-mode differentiation and its shortcomings

The single most undervalued fact of mathematics: matrices mathematical expressions are graphs, and graphs are matrices.

Yes, I know. You already heard this from me, but hear me out. Viewing neural networks — that is, complex mathematical expressions — as graphs is the idea that led to their success.

Computationally speaking, decomposing models into graphs is the idea that fuels backpropagation, the number one algorithm used to calculate the function's gradient. In turn, this gradient is used to optimize the model weights, a process otherwise known as training.

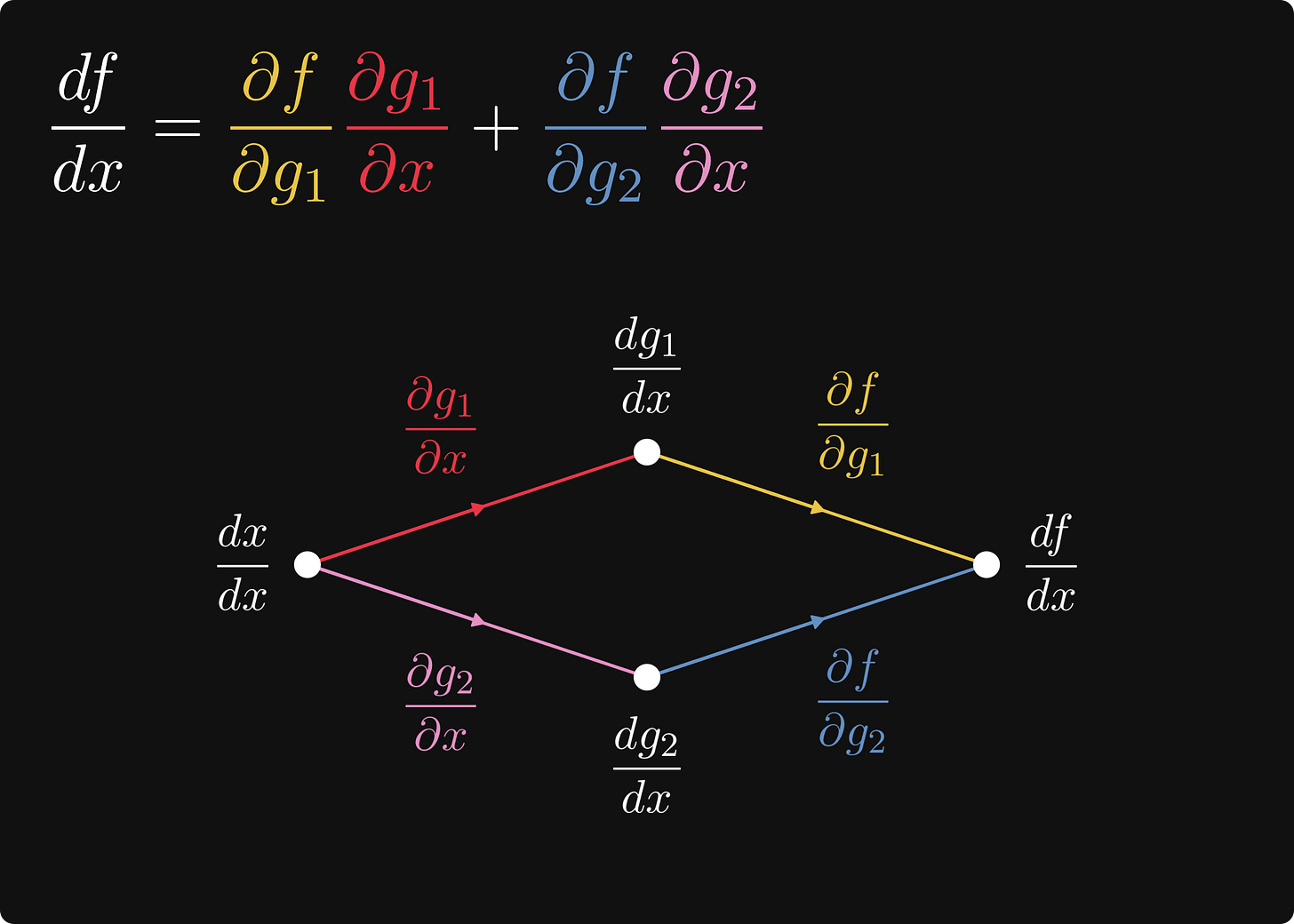
Take a look at this illustration below: this is the omnipotent chain rule in computational graph form.

This post is dedicated to explaining exactly what's going on in this picture.

So, you want to compute the derivatives of computational graphs. To make things concrete, we'll use a familiar example, the logistic regression.

In mathematical terms, logistic regression is defined by the function