Computational Graphs and the Forward Pass

Reverse-engineering the computational graph interface

Now that we understand how to work with computational graphs, it's time to pull back the curtain and see how they work on the inside. After all, this is what we're here for. (At least, it's why I'm writing this.)

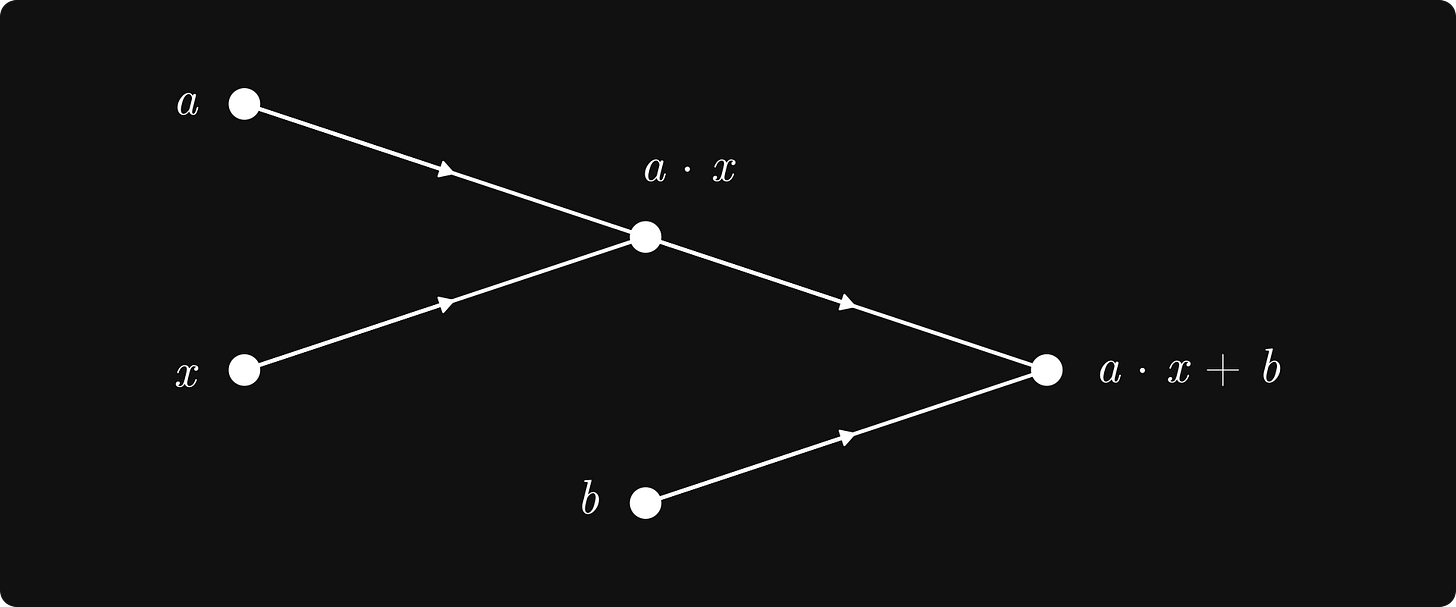
A quick recap: a computational graph is the graph representation of a mathematical computation. By considering the order of operations, we can represent any expression in a graph form. For instance, here's the graph representation of ax + b.

It’s not just linear regression. Any neural network, no matter how large, can be described with a computational graph. Our goal is to implement them from scratch to gain a deep understanding of how they work.

The plan:

• understand how to work with computational graphs,

• and reverse-engineer the implementation.

For this purpose, I have built mlfz, an educational machine learning library, where computational graphs are represented by the Scalar class. You can simply define graphs by using expressions such as y = a * x + b, and compute the gradient