Min-Max Math, ep. 04: The (art and) science of reasoning
Introduction to mathematical logic
Last time, we delved into the depths of mathematics and glimpsed what’s there: axioms.
Our trip was quite psychedelic. Instead of a precise and technical treatment, we went the scenic route. The foundations are in place. Now it’s time to do some mathematics.
Previously, we have seen that theorems and proofs are the heart of mathematics. We’ve touched upon proofs, at least with a simple example. Now, it’s time to study them from a higher level. It’s time to learn the (art and) science of reasoning.
Welcome to Mathematical Logic 101.
Important: it seems that the math blocks are bugged on the Substack website. If you click anywhere near them, they fall apart and leak the LaTeX source. Like this:
You can reset these blocks by reloading the page.
Statements, true or false
“It’s raining.”
“The sidewalk is wet.”
“There are infinitely many prime numbers.”
In mathematical logic, we are interested in statements. A statement can be either true or false; this is called its truth value. At least in classical logic. We’ll deal with the extensions of logic later. If you are interested in more, the very first post of The Palindrome is about this:
The science of science
It’s 6:00 AM. The alarm clock is blasting, but you are having a hard time getting out of bed. You don’t feel well. Your muscles are weak, and your head is exploding. After a brief struggle, you manage to call a doctor and list all the symptoms. Your sore throat makes speaking painful.
In computers, true is represented by 1, and false is represented by 0.
All mathematical results are true propositions. It’s that simple.
Thanks for reading my Min-max Math course. See you later!
If you’re still here: no, it’s not that simple. There are two components missing. First, the reason why modern science is so powerful is analytical thinking; that is, our ability to disassemble complex systems into its simpler parts and reason about them separately. In other words, complex propositions are composed from simpler ones via logical connectives.
Second, we need more tools to deduce the truth value of a statement.
Let’s talk about connectives first.
Logical connectives
“The sky is blue and the grass is green.”
“The ReLU function is not differentiable at zero.”
“The entropy of a closed system cannot decrease.”
The entire body of human knowledge is stored in the form of true propositions. To reason about complex propositions effectively, we’ll introduce operations to disassemble and combine them. These operations are called logical connectives, and the four most important are
NOT (¬), also known as negation,
AND (∧), also known as conjunction,
OR (∨), also known disjunction,
and THEN (→), also known as implication.
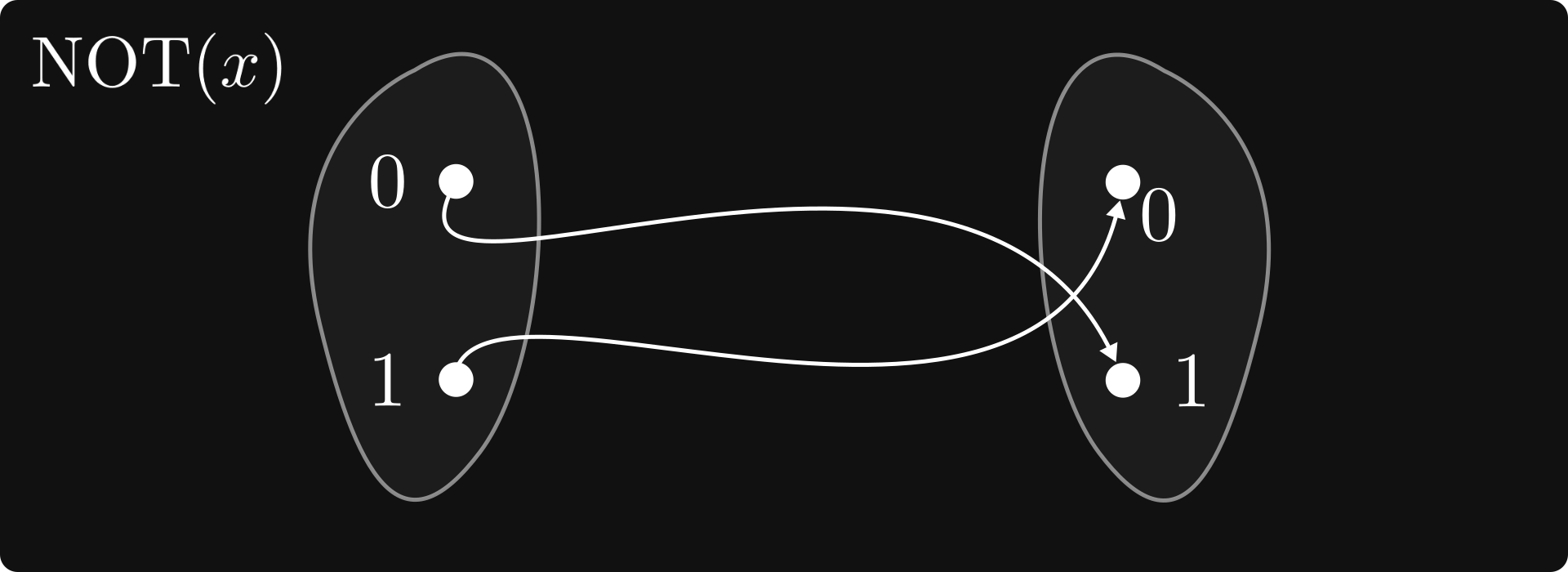
Connectives are defined via the so-called truth tables. It’s easier to see an example. Let’s start with the simplest one: negation.
Thus, by definition, NOT A is true precisely when A is false.
You can think about NOT as a function that maps true to false and false to true. Or 1 to 0 and 0 to 1. (We haven’t talked about functions before, so don’t get hanged up at the exact definition. I promise, we’ll study functions in great detail later.)
What’s the negation of “the wall is white”? Take a second to figure it out.
The solution is simply “the wall is not white”. (And not “the wall is black”, as I thought as a high school student. We all learn from our mistakes.)
Let’s move on to AND and OR, two of the most commonly used connectives. They formalize what you expect: “and” and “or”.