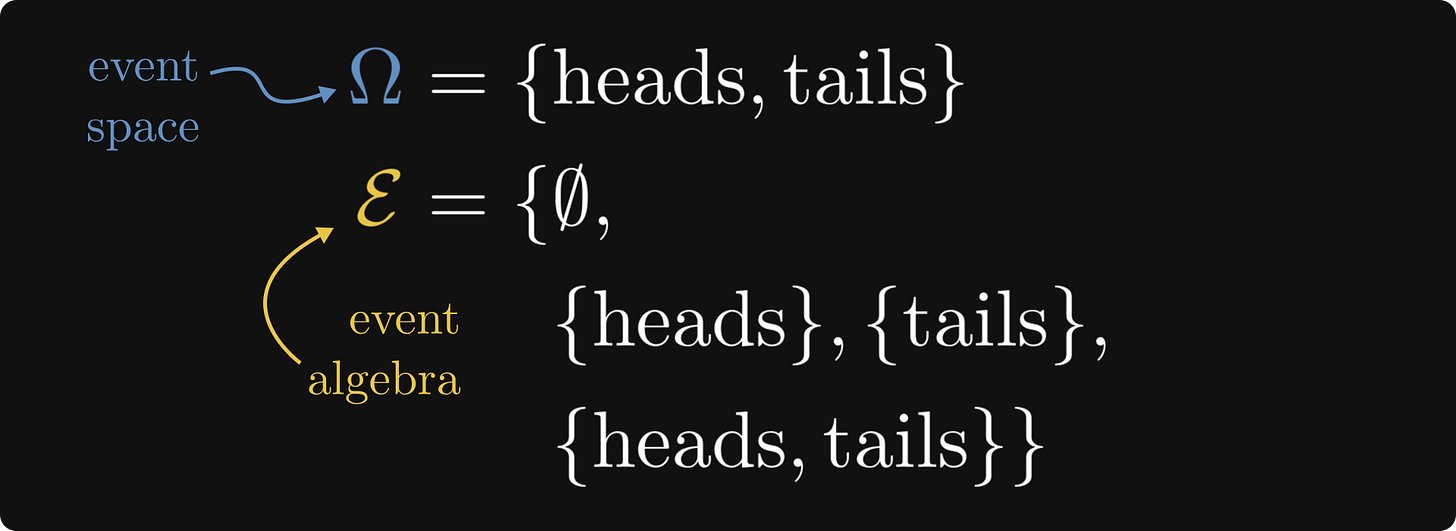Machine learning is not just statistics

Discussing the differences, the similarities, and the nuances

Two of the most common misconceptions I hear:

“Machine learning is just applied statistics.”
“Statistics is just applied probability.”

Like all proper misconceptions, these are rooted in truth as well. Machine learning heavily utilizes statistics, and statistics is built upon probability theory.

However, there are fundamental differences in the mindsets.

Probability enables us to reason about uncertainty; statistics quantifies and explains it. Machine learning makes predictions from data. It might use probability and statistics. It might not.

This post is about the differences, the similarities, and everything in between. Because these classes are definitely not linearly separable.

One thing is sure: probability is where it all starts.

---

This post is the next chapter of my upcoming Mathematics of Machine Learning book, available in early access.

New chapters are available for the premium subscribers of The Palindrome as well, but there are 40+ chapters (~450 pages) available exclusively for members of the early access.

---

Probability

Once upon a time, Newton invented calculus. An apple fell on his head, and soon, he had a method to compute the trajectory of said apple. Or a thrown rock. Or an orbiting space station.

However, compared to an orbiting space station, predicting the outcome of a tossed coin is extremely hard. Think about it: a space station orbits in vacuum, but the coin is flying in the air. From a physical perspective, vacuum is a much simpler ambience. No complex hydrodynamical forces, no turbulence, no chaos.

Nowadays, we can precisely compute the trajectory of a falling coin, but this was not the case in the 18th century, when probability theory came to life. Mind you, it was started by a few aristocrats looking for an edge in their gambling adventures.

Antoine Gombaud, chevalier de Méré wanted to play a game, but he accidentally launched an investigation that gave birth to one of the most essential tools. One that became the logic of science.

Think of probability as a means of dealing with missing information. Probability theory provides the tools to formulate and deal with such models. To illustrate this principle, let’s see the simplest possible example, one that we already talked about: tossing a coin.

Let’s build a probabilistic model! What makes one? Probability is a measure of likelihood for the so-called events. In our case, the events are the potential outcomes, i.e. heads or tails.

That is, the event space is modeled by a set, and the events by subsets of the event space.

There are three simple rules that any measure of probability must satisfy:

1. the probability is a nonnegative number between 0 and 1,

2. the probability of Ω is 1,

3. and the probability of mutually exclusive events sum up.

These are called Kolmogorov’s axioms.

Because the outcome of a coin toss is perfectly random, it is safe to assume that the probability of heads and tails is the same. With this, our probabilistic model is complete.

caption...

Probability theory allows us to reason within the confines of this model. What is the probability of getting five heads after tossing it up ten times?

(If you are interested in more about probability and why it is the logic of science, check out the very first post of this newsletter.)

However, assigning probabilities to our probabilistic models is a different question. How do we solve that?

Enter the world of statistics.