The Computer Scientist's Guide to Graph Theory, ep. 00
Or what do your brain, your friends, and the city you live in have in common
Hi there! This post is a collaboration with Alejandro, taken directly from our upcoming book, The Hitchhiker's Guide to Graphs. This project grew out of our series in graph theory here, aiming to focus on the algorithmic aspects as well. We'll even implement our custom graph library from scratch.
The book is already available in early access, with instant updates to the content as we write it.
Alejandro is one of my favorite writers and one of my original inspirations for starting to talk about mathematics online. We complement each other in knowledge and style: He is a master of computer science and algorithms, and I make the necessary theoretical background as clear as possible.
If you would like to see what's the book like, check out our introductory series on graph theory:
Episode 00: What do your brain, your friends, and the city you live in have in common
Episode 01: Running into the woods: trees, forests, and spanning subgraphs
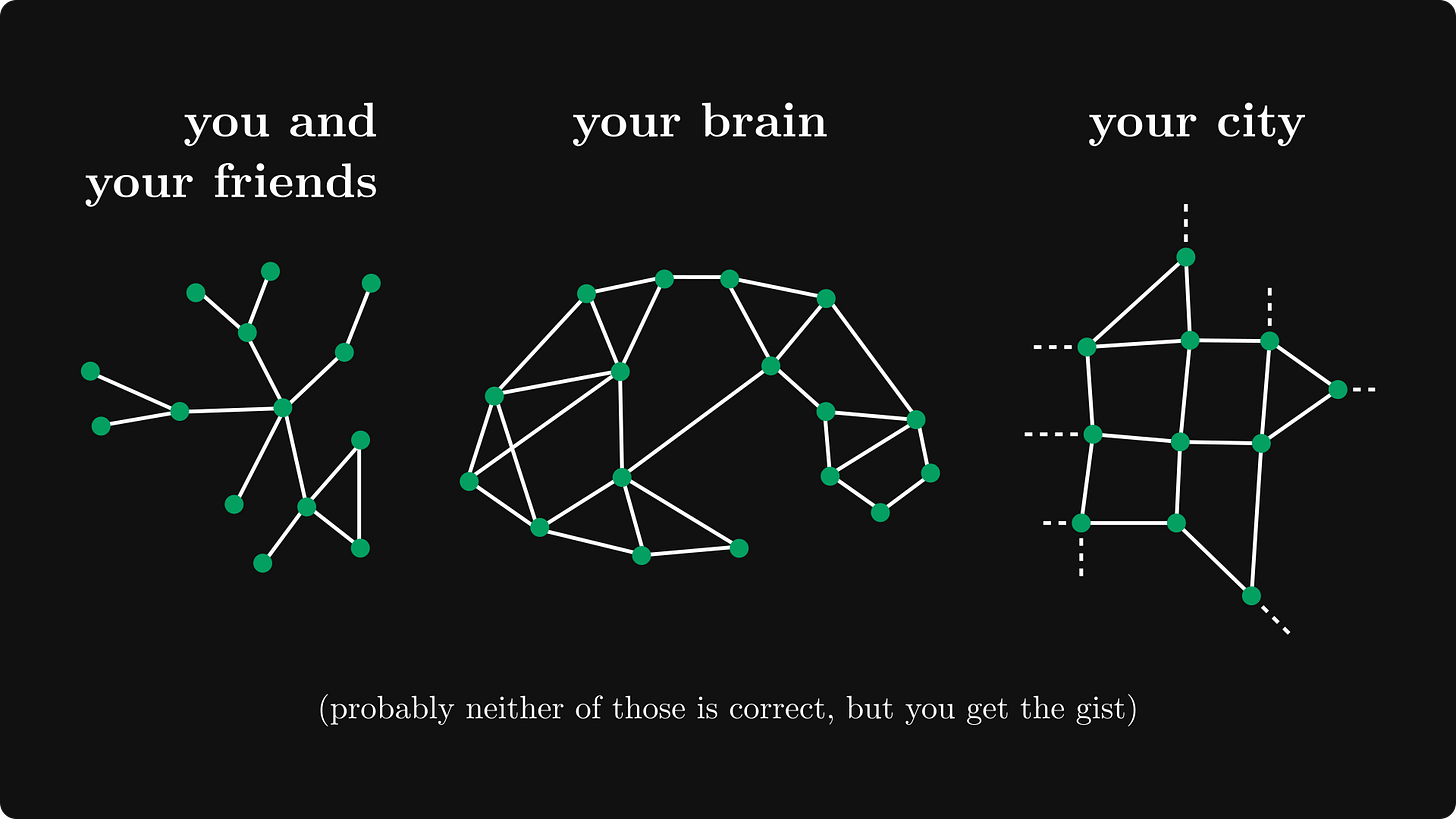
What do the World Wide Web, your brain, the corpus of scientific knowledge accumulated by all of humanity, the entire list of people you’ve ever met, and the city you live in have in common?
These are all radically different concepts, from physical, to virtual, to social in nature, but they share a common trait. They are all networks that establish relationships between objects.
Think about it.
The World Wide Web is a network of interconnected computational resources.
Your brain is a network of interconnected neurons.
The accumulated knowledge of humanity is a network of interconnected ideas. (All discoveries depend on prior knowledge, and unlock potential new discoveries.)
The city you live in is an interconnected network of roads and buildings. And the people you know are also a network, as many of them know each other, or know someone who knows someone you know.
As distinct as these things seem to be, they all share common properties by virtue of their networked nature. For example, you can think of how “close” two objects in a network are. The meaning of “distance” will be different if you’re considering
physical networks (like roads)
versus information networks (like published papers with citations to other papers)
versus social networks (like your Facebook friends),
but in all cases, there is a sense in which some objects are “close together” or “far apart”.
There is a philosophical school of thought called structuralism, which was very prominent throughout the 20th century. Structuralism emphasized that the way things are connected is a fundamental part of their essence. In a structural sense, everything is defined in terms of how it interacts with other things.
In a similar vein, one of the most prominent paradigms in cognitive science, connectionism, champions the idea that simple connected objects—like neurons—can give rise to complex phenomena—like thought.
What if we could study this abstract notion of networks of interconnected elements, and understand the fundamental properties of all sorts of networks all at once?
This is the purpose of graph theory.
A graph is a mathematical abstraction that captures the fundamental notion of things connected together. Graph theory is the branch of mathematics — more specifically discrete mathematics — that studies graphs from a theoretical point of view. It is one of the most fascinating branches of math, science, and human knowledge in general.
We’re here to open a window for you to dive into this universe.
This is the first in a series of five articles introducing the foundational ideas in graph theory, written by Alejandro Piad Morffis and illustrated by Tivadar Danka.
In this series, we will learn the vocabulary of networks and connections in a wide variety of domains, plus some of their mind-blowing properties. We will also learn a thing or two about constructing proofs in discrete math, which is a fascinating subject on its own.
There are absolutely no prior requirements to get the most out of this series, other than a bit of bravery and a lot of curiosity. While the series is not algorithm-oriented, the intuitions we build here will serve as the foundation for a subsequent series on graph algorithms that we’re planning for next year.
(To satisfy all readers, we will always provide all the intuitive ideas behind the fundamental concepts and results presented in each article, plus optional sections regarding the technicalities. So, the math-savvy among you will find the nitty-gritty details, but these are not necessary to understand and enjoy the rest of the content.)
If this sounds enticing to you, buckle up. Some math is coming!
The basic concepts of graph theory
The most important concept in graph theory is the graph itself.
Intuitively, a graph is just a (finite) collection of elements — vertices, or sometimes nodes— connected by edges. Thus, a graph represents an abstract relation space, in which the edges define who’s related to whom, whatever the nature of that relation is.
We can formalize the notion of a graph using the tools from logic, which gives us the precise notation and formalism to define graph as a definite mathematical object.
We can say a graph is an object composed of two sets: one set of elements we call vertices, and another set of elements we call edges, with the detail that edges themselves are nothing but sets of two vertices. Thus, in principle, there is nothing about an edge that matters beyond which two vertices it connects (we will see this isn’t exactly the case when we examine some special types of graphs.)
Formally, we can define a graph as the following.
Definition 1: A graph G = (V, E) is a collection of two sets, a set of vertices V, and a set of edges E ⊆ V × V.
(When graphs are given without specifying the sets of vertices and edges, we can use the notation V(G) and E(G) respectively to refer to these components in an arbitrary graph G.)
Graphs are abstract objects, which means they don’t have an intrinsic visualization. However, we can visualize graphs by drawing dots for vertices and lines for edges. An example of a simple graph is shown below.
This graph is composed of the vertices a, b, c, d, e, and the edges ab, ae, bc, bd, cd, ce, de. (Instead of properly denoting edges like (a, b) ∈ V × V, we’ll remove the fluff and shorten them to ab.)
There is nothing intrinsic to names or exact locations of the vertices in the drawing. Except in very concrete cases — such as when a graph represents a geometrical or geographical object — the layout of a graph is arbitrary, and thus, the same graph can be represented in an infinite number of ways. (Which is illustrated on the figure below.)
The most important characteristic of a vertex is its degree. The degree of the node v, denoted by deg(v), measures the number of edges that touch v.
For example, deg(a) = 2, as only the edges ab and ae connect a with another vertex. In contrast, the remaining vertices all have degree 3. We name the set of vertices connected to an arbitary vertex v its neighborhood, denoted by N(v). Thus, the neighborhood of c is {b, d, e}.
It should now be self-evident that the degree of a vertex is the size of its neighborhood.
Formally, we will write N(v) to refer to the neighborhood, and deg(v) = |N(v)| to refer to the degree of any vertex v ∈ V(G).
Walking through a graph
In the study of networks, indirect connections are as important as direct ones. Speaking in the language of graphs, indirect connections are formalized by walks. A walk is simply a finite sequence of connected nodes.
For example, (a, b, a, e, c, d) is a valid walk in our example graph, that happens to go though all vertices, but this, of course, isn’t necessary. Notice that we can move over the same edge back and forth as we want, so we can extend any walk infinitely.
If we never repeat an edge, then we have a trail. The previous walk is not a trail because we backtrack through ab. In contrast, (a, e, c, d, e) is a valid trail in our example graph, because although e appears twice, we get to it via different edges each time.
Finally, if we also never repeat a vertex, then we have a path (some literature will use path to refer to what we call a trail, and simple path to refer to a path with no repeated vertices). In our example graph, (c, d, e, a, b) is a path that happens to involve all vertices.
However, if the path loops over from the final vertex back into the first one, so the start and end are the same vertex, we call it a cycle.
Proving our first theorem
You might have noticed that the difference between a trail and a path is that trails can have cycles inside them. Can we define a path as a trail without cycles? Yes.
Let’s prove our first theorem!
Theorem 1. A path is a trail without a cycle.
Proof. Let p = (p₁, p₂, …, pₙ) be an arbitrary walk. Theorem 1. is two theorems in one.
If p is a path, then p doesn’t contain a cycle.
If p is a trail that doesn’t dontain a cycle, then it is a path. (That is, a walk without repeated vertices.)
We’ll prove Theorem 1. by proving both, starting with the first one.
If p is a path, then p doesn’t contain a cycle. This is easy to see, as cycles contain a repeated vertex. The presence of a sub-cycle would mean that our path is not a path after all. (As paths are not allowed to have repeating vertices.)
Let’s analyze this statement further! If we introduce a snippet of formal logic and let A and B denote the propositions
A: p is a path,
B: p doesn’t contain a cycle,
then the first part of our theorem is the same as “if A, then B“, that is, A → B.
Instead of merely showing A → B, what we did was to show ¬B → ¬A. This is called the principle of contraposition, and it’s popping up in mathematics more frequently than whack-a-moles in a carnival row. In fact, we’ll use contraposition to show the second part!
If p is a trail that doesn’t contain a cycle, then it is a path. By contraposition, this statement is equivalent with the following:
If p = (p₁, p₂, …, pₙ) is not a path (that is, it contains at least one repeated vertex), then it contains a cycle as well.
Let’s go!
As p = (p₁, p₂, …, pₙ) contains a repeated vertex, say v, let (v, v₁, …, vₘ, v) be the looping sub-trail.
Is (v, v₁, …, vₘ, v) a cycle? If the answer is yes, we are done. If not, then by the definition of the cycle, there is another looping sub-trail (w, w₁, …, wₖ, w). This time however, the newly obtained sub-trail is strictly smaller, than (v, v₁, …, vₘ, v).
Is (w, w₁, …, wₖ, w) a cycle? If the answer is yes, we are done. If not, then by the definition of the cycle…
You get the pattern. Can we continue to get “no” as an answer infinitely? No, because our original trail is finitely long, and each iteration finds a strictly smaller sub-trail. Thus, eventually, we obtain a cycle, which is what we had to show.
With that, our proof is complete. ■
(The square ■ denotes the end of a proof, short for quod erat demonstrandum, i.e. this is what we had to show.)
Taking these ideas a step further, we quickly arrive to a conclusion that if we can get from a to b in a graph, then we can get from a to b without repeating a vertex.
Why? Intuitively, every time we find a cycle on our way from a to b, we can skip it and continue directly on the “main path”. Thus, it makes sense to think that we can always remove all detours from a trail and extract a path that begins and ends in the same vertices. If we can get from a to b at all, then we must be able to get from a to b without making any unnecessary loops, right?
Meet our second theorem.
Theorem 2. In any graph G, if there is a trail from a to b, then there is a path from a to b.
Proof. Let’s repurpose our trimming idea from the second part of Theorem 1.’s proof. Suppose that we are given a trail from a to b. Does it contain a cycle?
If not, then we have a path; as Theorem 1. claims that paths are trails without cycles. If yes, we can trim that cycle.
Again, can we continue to trim cycles forever? No, as the original trail is finite. Thus, we are guaranteed to stop, obtaining a trail without cycles. That is, a path. ■
(Note that by the same previous argument, if you directly consider the shortest trail between a and b, that must be a path — otherwise you could make it shorter. This is a slightly different way to prove Theorem 2., but based on the same principles.)
Connectivity in graphs
Vertices and edges are the building blocks of graphs, which give rise to walks, trails and paths. With these notions, we can start to ask general questions about the structure of a graph. One such question regards connectivity, that is, which vertices are reachable from each other.
We say a graph is connected if there is a path between all pairs of vertices (actually, now we know we only need to find a trail). The example graph we’ve been using so far is connected, as well as the graph that represents streets in your city, or your Facebook friends.
However, the graph of all roads in the world is not connected, as there are places you can’t travel by land. Such disconnected graphs are still always composed of connected sub-graphs, which call connected components — small islands of vertices that can be reached from each other.
Thus, a connected graph has exactly one connected component. A graphs can have up to n = |V| components — one for each vertex, if there are no edges.
An interesting question regarding connectivity is how critical a vertex or edge is in ensuring some part of the graph is reachable. If removing a single vertex (or edge) from a graph splits a connected component into two or more, then that vertex is called a cut vertex (or cut edge).
In the previous graph, the removal of vertex a (and its corresponding edges) produces five connected components, while the removal of vertex b produces three. The removal of the edge ab only produces two connected components.
Removing a vertex can split a connected component into as many as there are remaining vertices in the graph. (Think of a graph in the shape of a star, one vertex connected to all the rest.). However, the removal of any single edge can at most split a component into two. This is an important result that we will use in future posts to prove some very powerful theorems.
If a graph is such that no single vertex (or edge) removal can disconnect it, we call it bi-connected. This concept will be essential for us later this series.
Final remarks
So far, we’ve been talking about undirected graphs; that is, graphs where edges are links, not arrows. Say, the graph of your Facebook network is undirected (as the “Facebook friend” relation is mutual), while the graph of your Instagram followers is not. (As you might not follow back everyone.)
Thus, we can either say the edge ab or the edge ba is in the graph, because both are exactly the same edge, and it would be redundant —and incorrect— to mention them both.
However, in some applications it is interesting to give a direction to edges, and consider that ab is different from ba. For example, in modeling transportation networks, sometimes you have single-direction routes. These are called directed graphs and although in practical applications they are essential, the fundamental theory is almost identical to undirected graphs, so we will only mention them when there’s some relevant difference.
Now that we have laid out the foundational theory, we are ready to move on to specific types of graphs and some concrete problems. Next time, we’ll be looking at trees, arguably the most important data structure in computer science.















Loved this colab. Tivadar says he "illustrated" the article, but he did much more than those really cool graphics. He also made two critical changes to the core proof that completely changed how approachable and intuitive the proof is for all readers. Without that, this would be a much more convoluted article.