Why is the Golden Ratio Hiding in the Fibonacci Sequence?
The non-recursive formula for Fibonacci numbers
The Fibonacci numbers form one of the most famous integer sequences, known for their close connection to the golden ratio, sunflower spirals, the mating habits of rabbits, and several other things.
Because of its recursive nature, computing the Fibonacci sequence via brute force is computationally expensive.
However, the Fibonacci numbers have a simple and beautiful closed-form expression written in terms of the golden ratio (φ) and the conjugate golden ratio (ψ).
In this post, we are going to derive it from first principles, learning two powerful mathematical techniques along the way: generating functions and eigenvalue decompositions.
Video version of the post:
If you enjoy my work, please support me by watching the video and leaving a comment! I just started a YouTube channel for my math explainer videos, so make sure to subscribe to not miss any of them!
First, let’s zoom in on the Fibonacci numbers.
The zeroth Fibonacci number F₀ is 0, the first Fibonacci number F₁ is 1, and by definition, the rest are given by the sum of the two preceding Fibonacci numbers.
Because of this, they grow insanely fast.
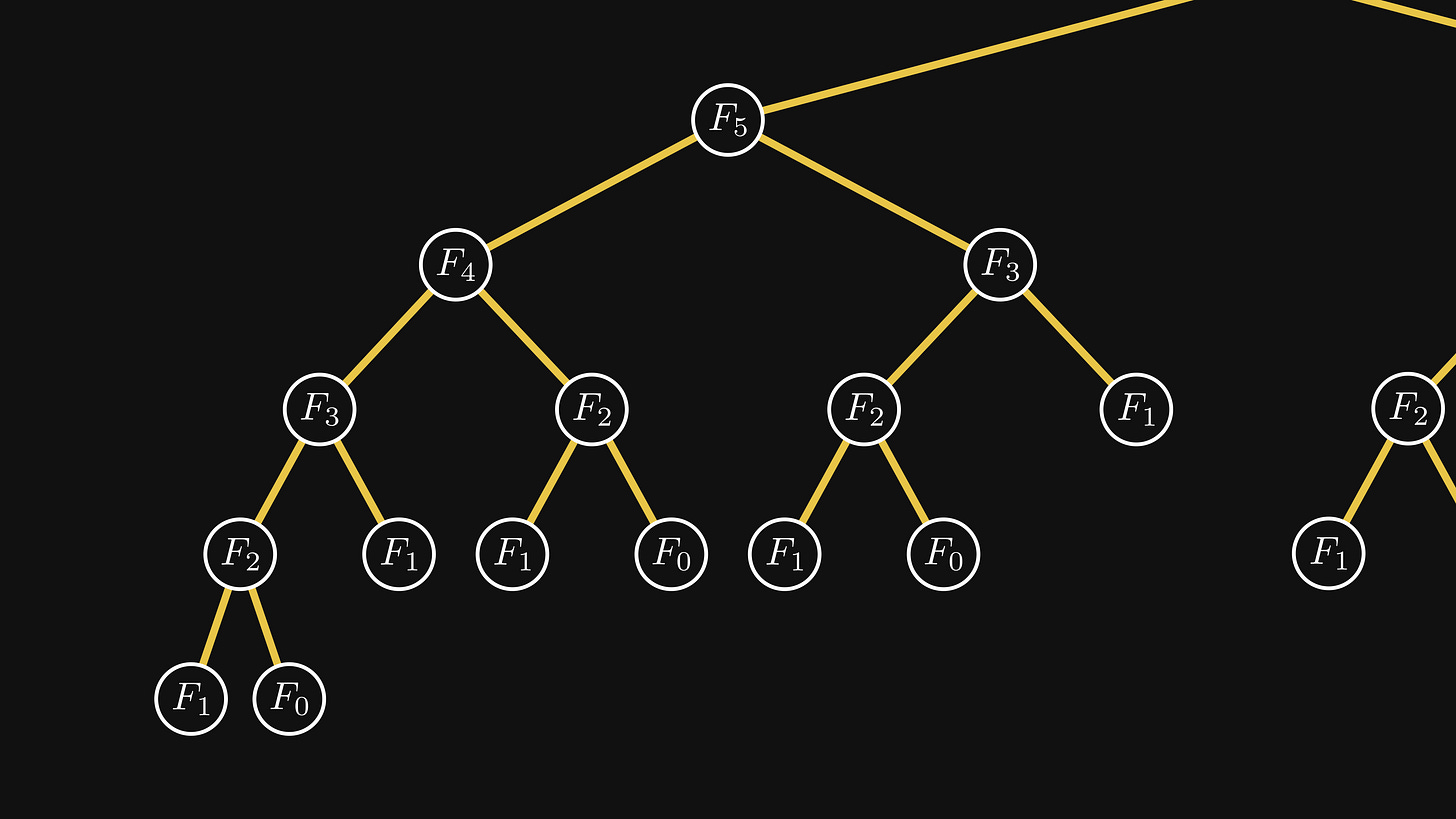
But that’s not the problem. Let’s take a look at what happens when we compute the Fibonacci numbers recursively.
F₀ and F₁ are given. These are our terminating conditions.
To find F₂, we compute F₁ and F₀;
to find F₃, we compute F₂ and F₁;
to find F₄, we compute F₃ and F₂;
and so on.
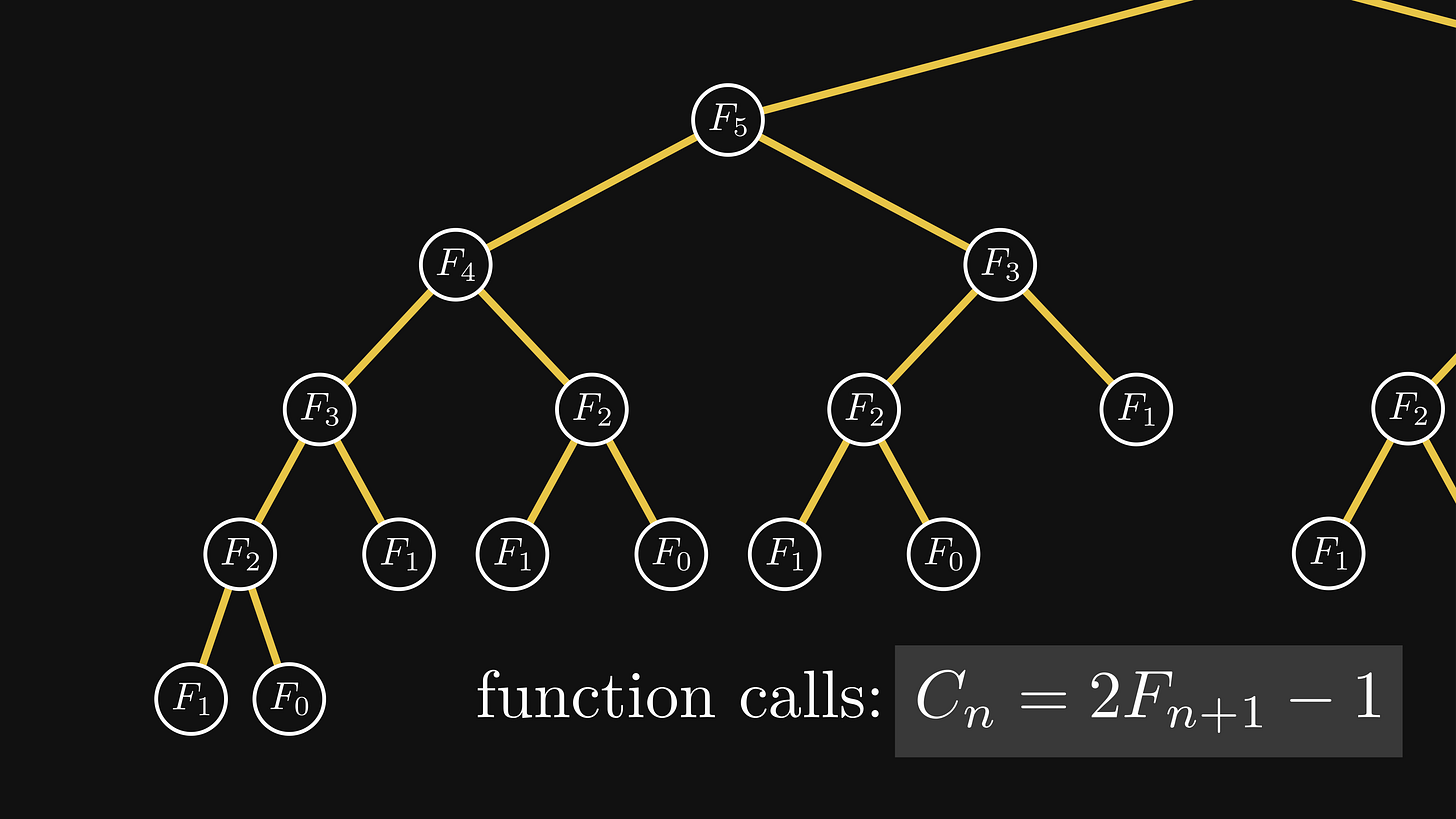
When computing the Fibonacci numbers recursively, the number of function calls also grows insanely fast.
How fast? Let’s see.
F₀ and F₁ require only one call, as they are terminating conditions.
F₂ requires 3 calls, F₃ requires 5, F₄ requires 9, F₅ requires 15, and so on.
In general, Fₙ requires 2 Fₙ₊₁ − 1 calls. This is a problem in practice.
How to solve it? First attempt: finding an explicit formula via generating functions.
But what are generating functions?
Suppose that we have a sequence aₙ, which we slap onto a power series as coefficients. The resulting expression is called the generating function of aₙ.
There are all sorts of potential issues raised by the convergence properties of power series, but we won’t deal with them.
For us, “a generating function is a clothesline on which we hang up a sequence of numbers for display,” as Herbert Wilf phrases it in his book generatingfunctionology. (Which is The Book on the subject.)
We are only interested in the combinatorial properties of generating functions.
Let’s see an example: the generating function of the binomial coefficients, which is given by the famous Newton’s binomial theorem.
Another example: 1 / n!, whose generating function is our good old friend, the exponential function.
One more example, the most important one for our purposes: the geometric series.
If we take qⁿ, multiply it by xⁿ, and sum over n, we obtain the rational function
1 / (1 - qx). q is called the quotient of the series.
Yes, I know: convergence and whatever, but let’s suspend our mathematical precision and go rock n’ roll with generating functions.
The generating function we want to study is the Fibonacci generating function, defined by F(x). How can we find an explicit formula for Fₙ with the help of F(x)?
Simple. If the generating functions for the sequences aₙ and bₙ are equal, then aₙ and bₙ must be equal as well.
Let’s get to work.
We start by unwrapping the definition of F(x), writing out the terms one by one:
Let’s focus our attention on the third term, F₂ x².
We can use the recursion here and write it as (F₀ + F₁)x².
Similarly, we can write the fourth term F₃ x³ as (F₂ + F₁)x³.
We can do this for all subsequent terms.
For simplicity, let’s unwrap the parentheses and write F(x) in a more suggestive form.
Now, the part F₀x² + F₁x³ + … can be written as x²(F₀ + F₁x + …).
Similarly, F₁x² + F₂x³ + ... can be written as x(F₁x + F₂x² + ...).
Lucky for us, both power series (in the parentheses) equal F(x). (Where we used the fact that F₀ = 0.)
Thus, we obtain the following functional equation:
We can simplify this even further. By arranging all the terms with F(x) on one side of the equation and divide both sides by the polynomial term 1 - x - x², we obtain the closed form expression of F(x).
We are at the finish line. I’m not going to spell out all the details, but with the magic of partial fraction decomposition, we obtain that F(x) is the linear combination of two familiar terms: the generating functions of geometric series.
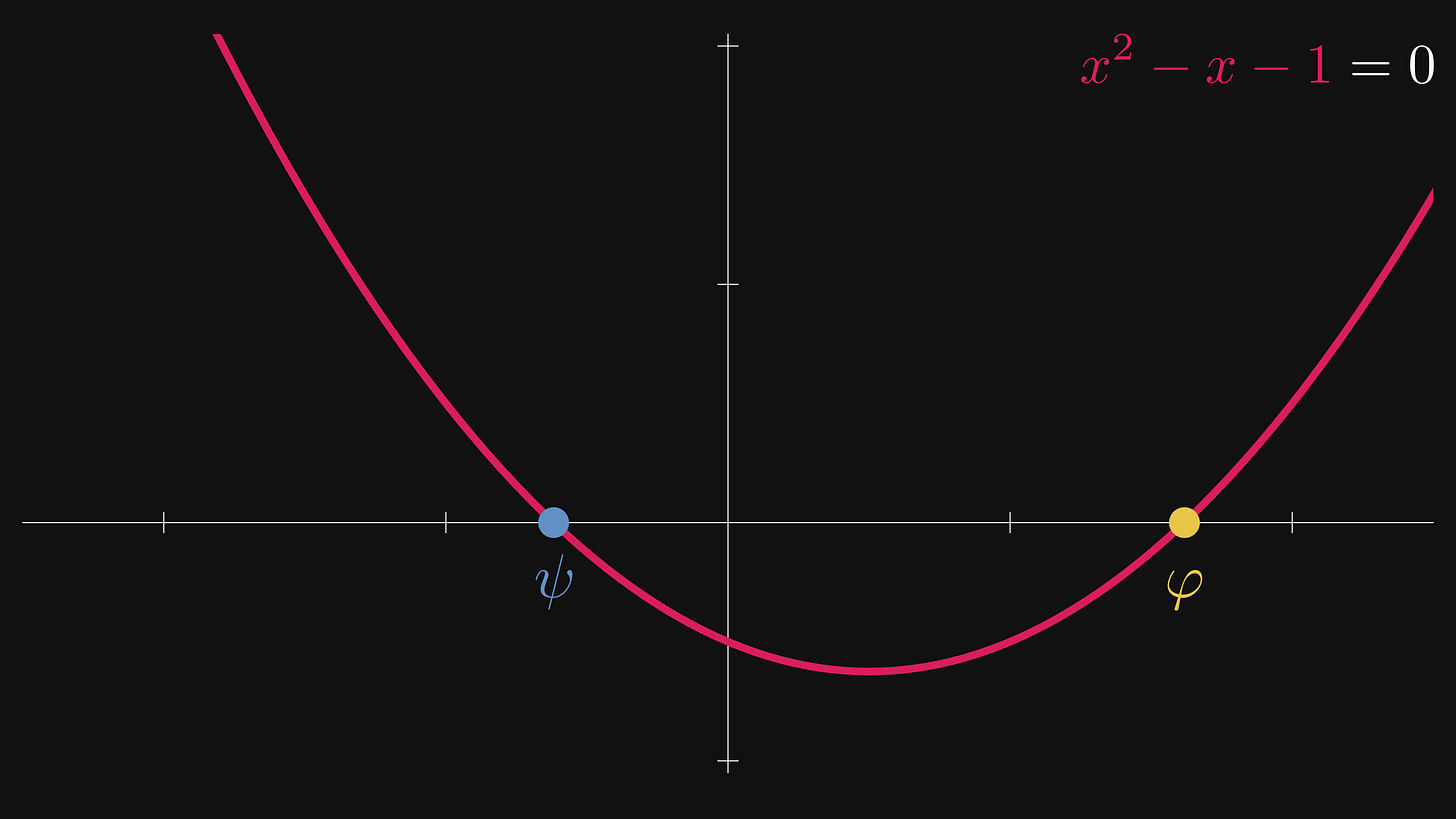
The quotient of the first term is (1 + √5)/2, otherwise known as the golden ratio. The quotient of the second term is (1 - √5)/2, otherwise known as the conjugate golden ratio.
(Note that the golden ratio minus the conjugate golden ratio is 1/√5.) Now, we can interchange the operations with the infinite sum to arrive at our desired formula.
Recall the most useful property of generating functions? Two generating functions are equal if and only if the underlying sequences are the same.
Now you see where we are going with this.
With generating functions, we obtain the well-deserved result: the non-recursive formula for Fibonacci numbers.
Even though generating functions are powerful and fun to use, I have to admit, we did a bunch of sketchy stuff to get here. I’m a mathematical analyst at heart, and I can’t just overlook issues like rearranging the terms of an infinite sum or interchanging it with operations.
So, what’s the solution?
I’ll show you another way; this time, with linear algebra.
Let’s talk about the Fibonacci matrix.
Let F be a simple 2 × 2 matrix: the first row is [1, 1]; while the second row is [1; 0].
I’ll spoil the surprise: the n-th power of F contains the Fibonacci numbers:
Here's a property of F that hints at what we are about to do: F is invariant to matrix transposition; that is, it is symmetric.
You guessed right: we are going to apply the spectral theorem for real symmetric matrices, otherwise known as the eigenvalue decomposition theorem.
This is an extremely powerful theorem, which we are applying to a simple problem. In mathematical terms, we are about to shoot a bird with a cannon.
Let's call this diagonal matrix D to simplify the towering computations that we are about to do.
Now, let’s square our matrix A using the eigenvalue decomposition.
As matrix multiplication is associative, we can eliminate the P’s in the middle,
Continuing this process, we find a convenient form for the powers of A.
Fortunately for us, computing the n-th power of a diagonal matrix is simple; we just have to raise the diagonal elements to the n.
Now, recall that the n-th power of the Fibonacci matrix is given by the Fibonacci numbers. Using the eigenvalue decomposition of F, we’ll eventually arrive at the non-recursive formula for the Fibonacci numbers.
Let’s get to work.
To compute the eigenvalues of F, we have to solve a quadratic equation given by the determinant of F - xI. This determinant is given by x² - x - 1.
By plugging the coefficients into the quadratic formula, we see that the roots of x² - x - 1 are given by the golden ratio (φ) and the conjugate golden ratio (ψ).
After crunching some numbers and matrices, we obtain the eigenvalue decomposition of F.
By raising it to the n-th power, we can already see the formula emerging.
We’ll unwrap the matrix products to compute the top-left element of the final product. (We don’t care about the others.)
By comparing the result of our computation with the n-th power of F, we get the desired formula.
Here it is once more in its full glory. Even though the non-recursive formula directly computes the n-th Fibonacci number, it involves working with floats, which introduces numerical issues. In practice, we are better off computing the powers of F.
However, if you think about it for a second, this is quite a remarkable formula. First, it establishes a precise relation between the golden ratio and the Fibonacci numbers. Second, even though the golden ratio and its conjugate are irrational numbers, the result is an integer.
In addition, it teaches us a valuable lesson on power series and symmetric matrices. When calculus, algebra, and combinatorics intersect, powerful tools can emerge.
Thanks for reading! Don’t forget to check the video version of the post:
If you enjoy my work, please support me by watching the video and leaving a comment! I just started a YouTube channel for my math explainer videos, so make sure to subscribe to not miss any of them!



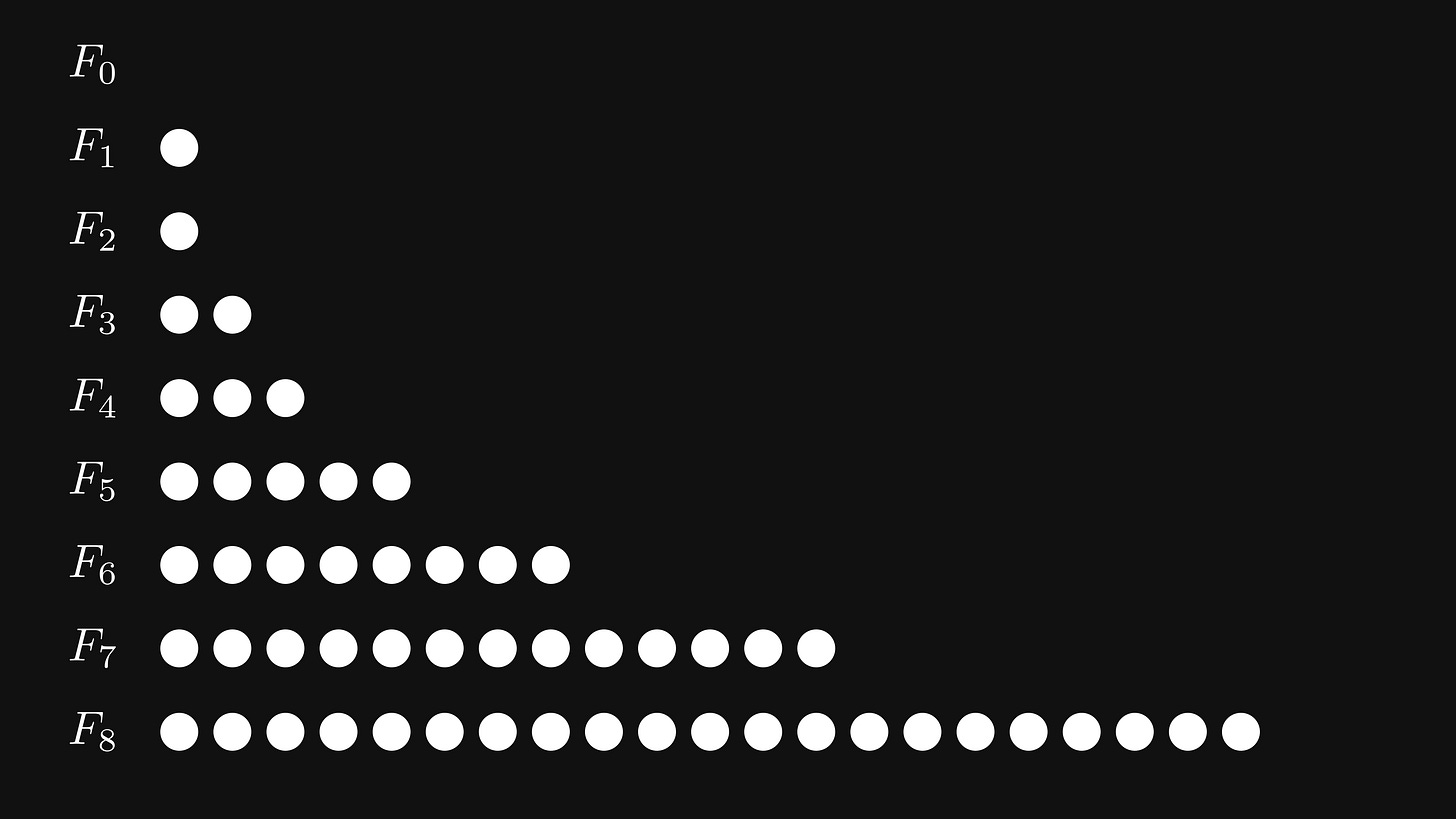
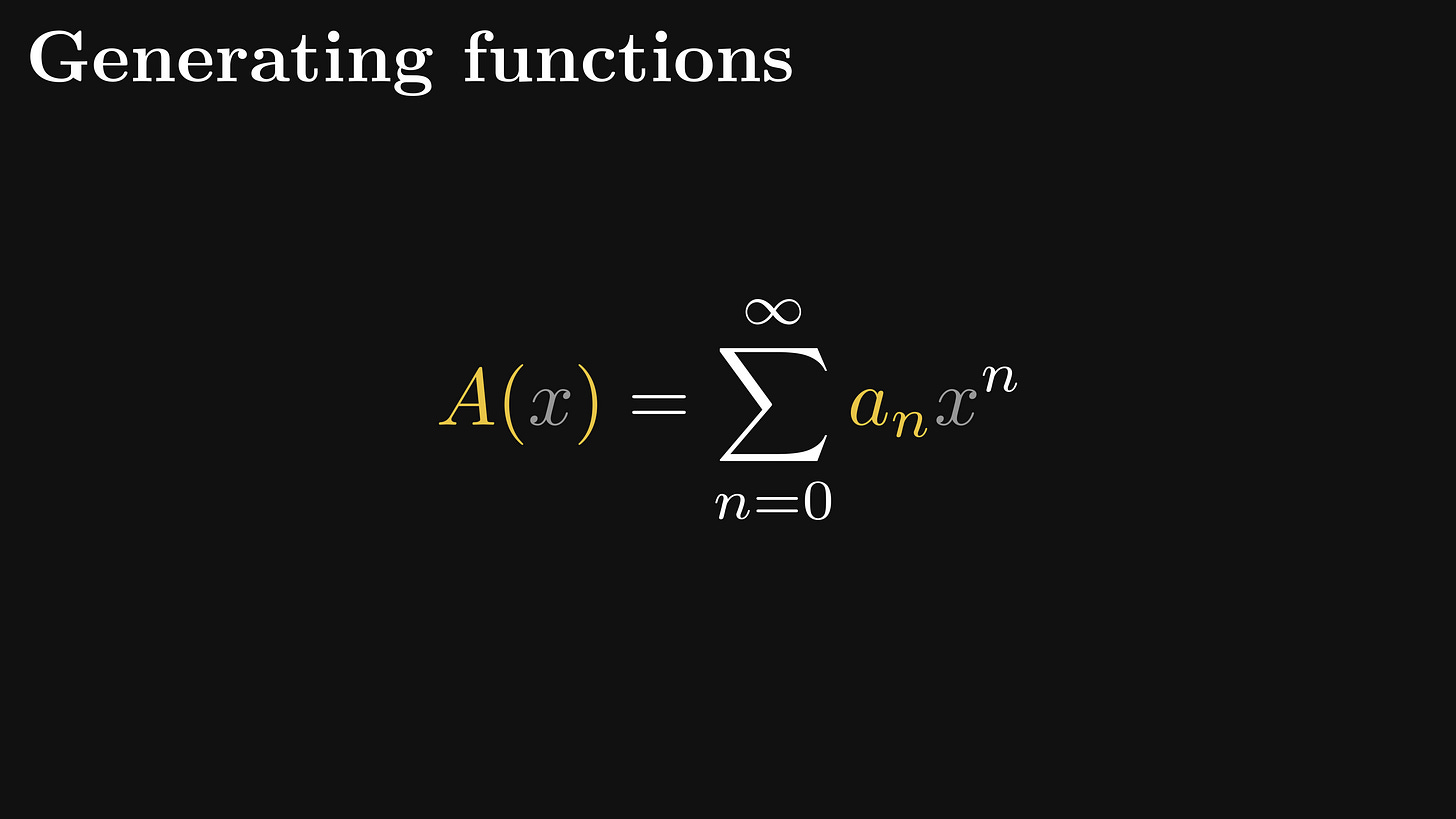

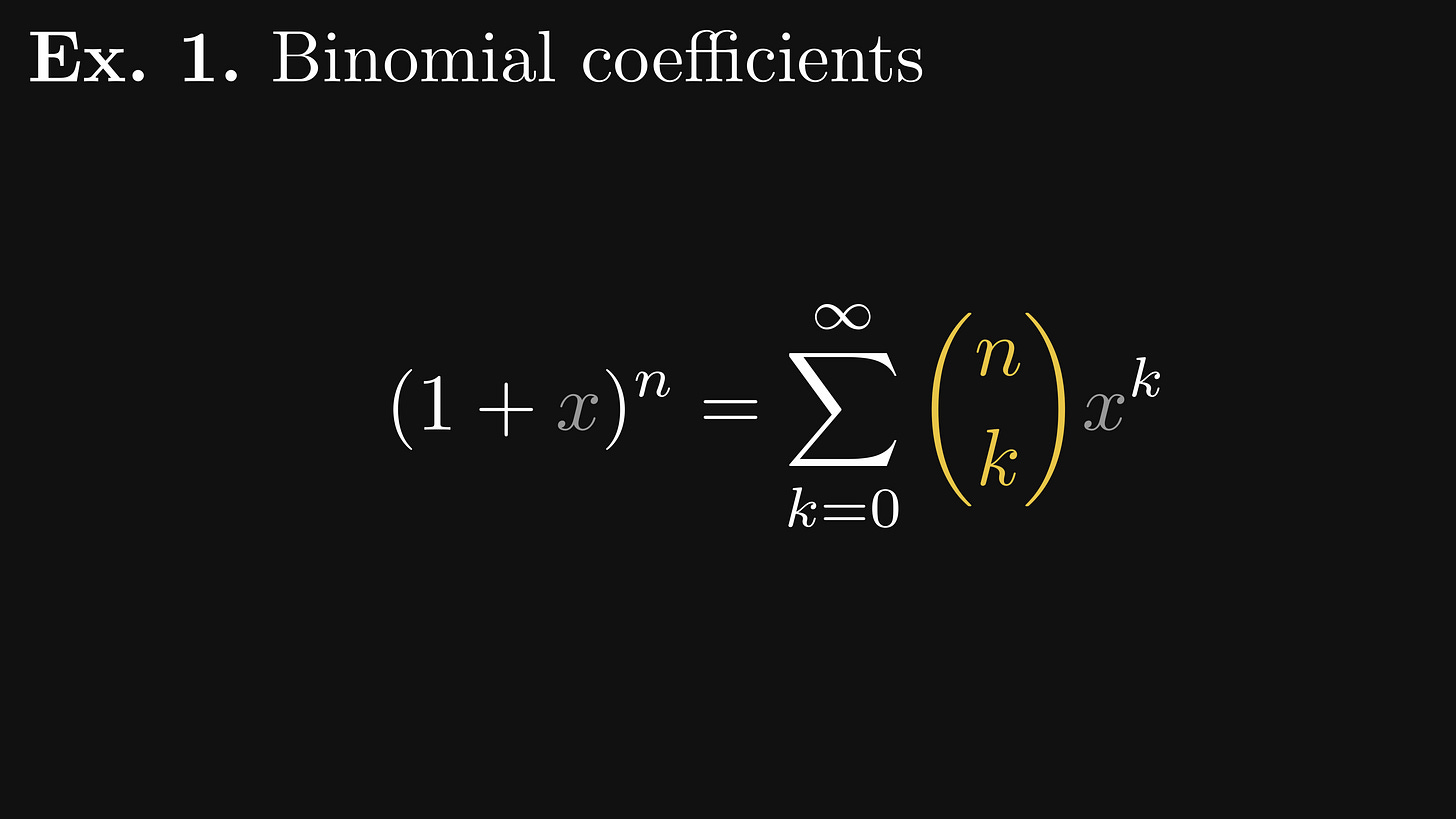
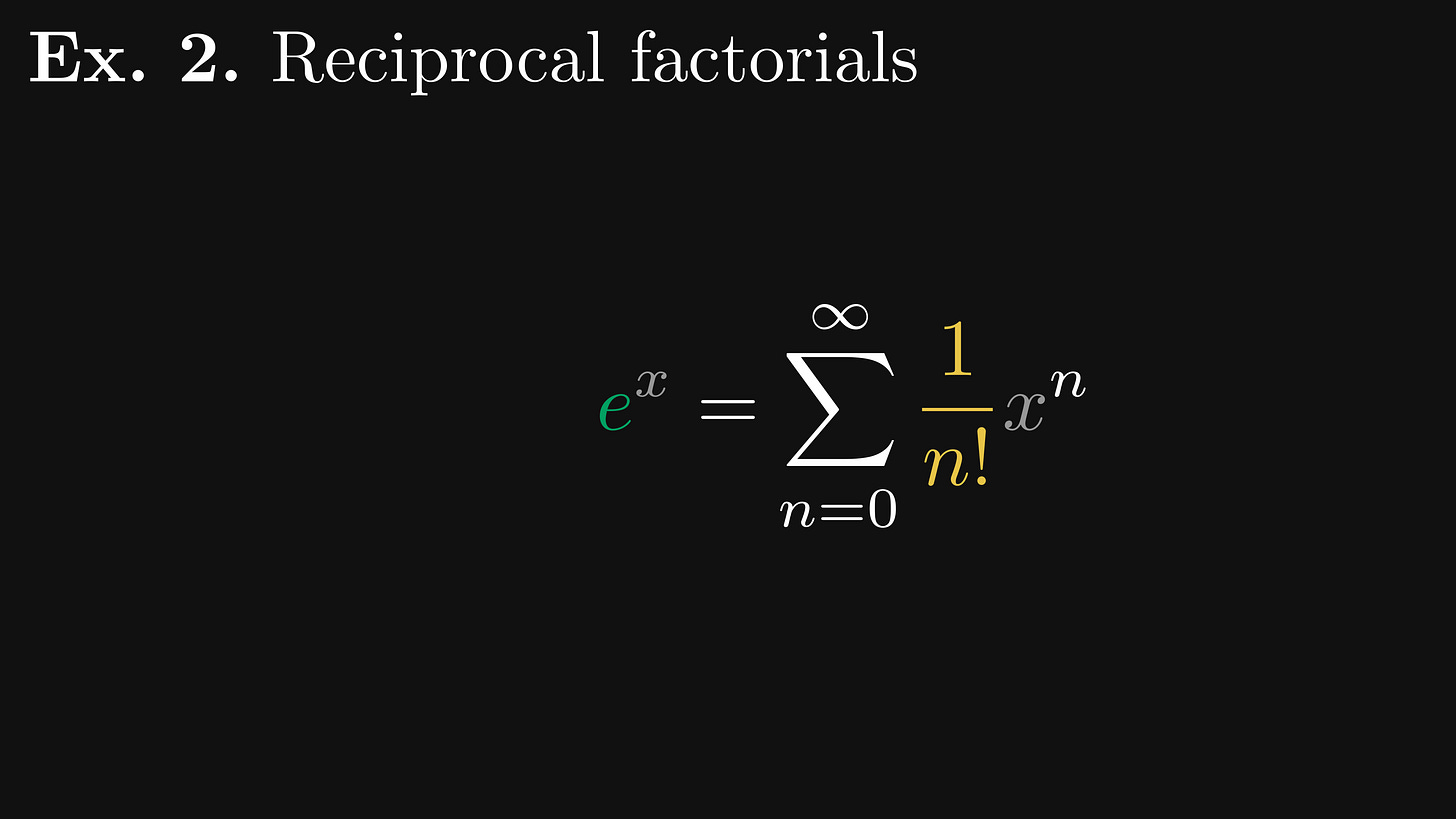
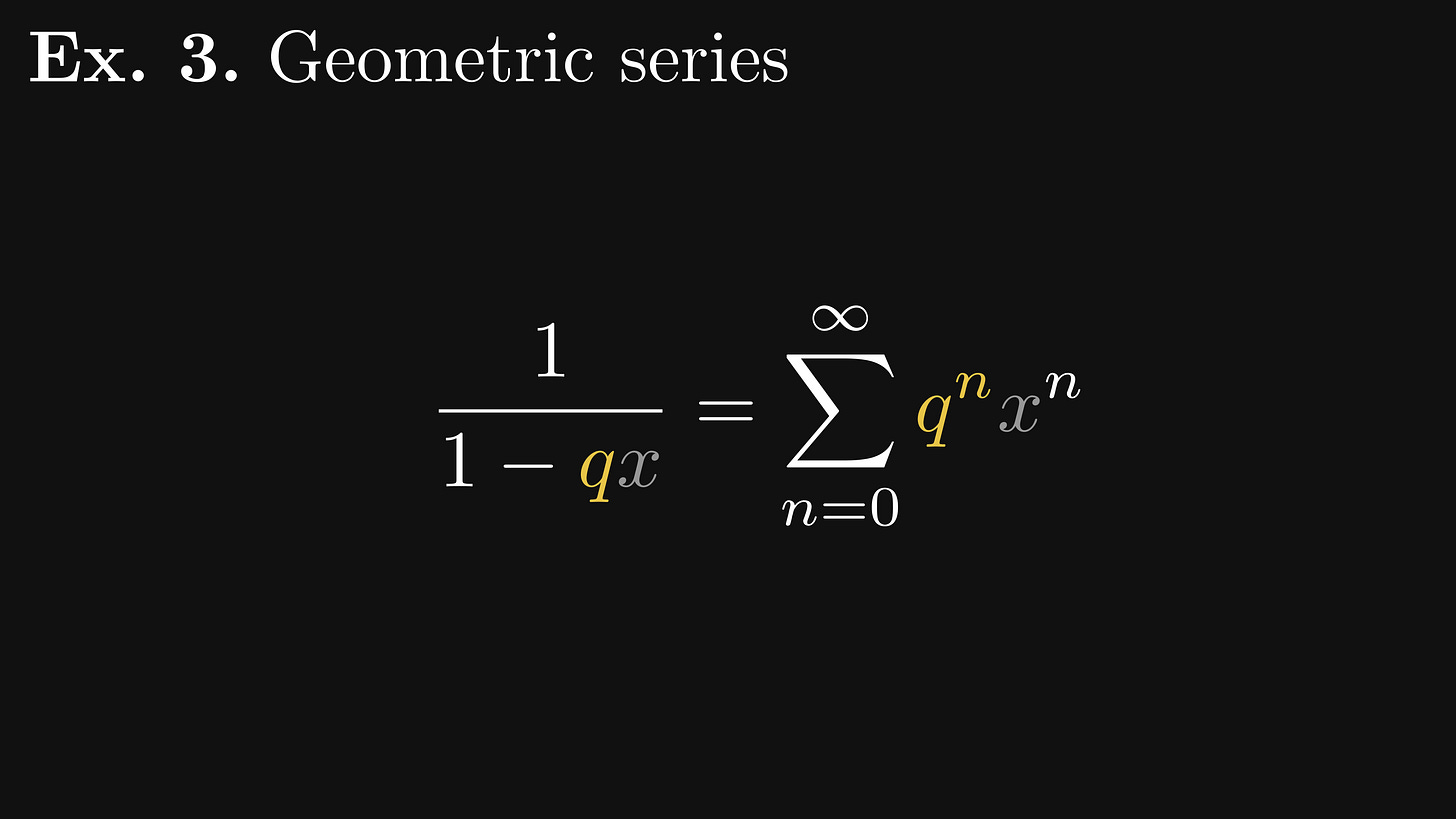
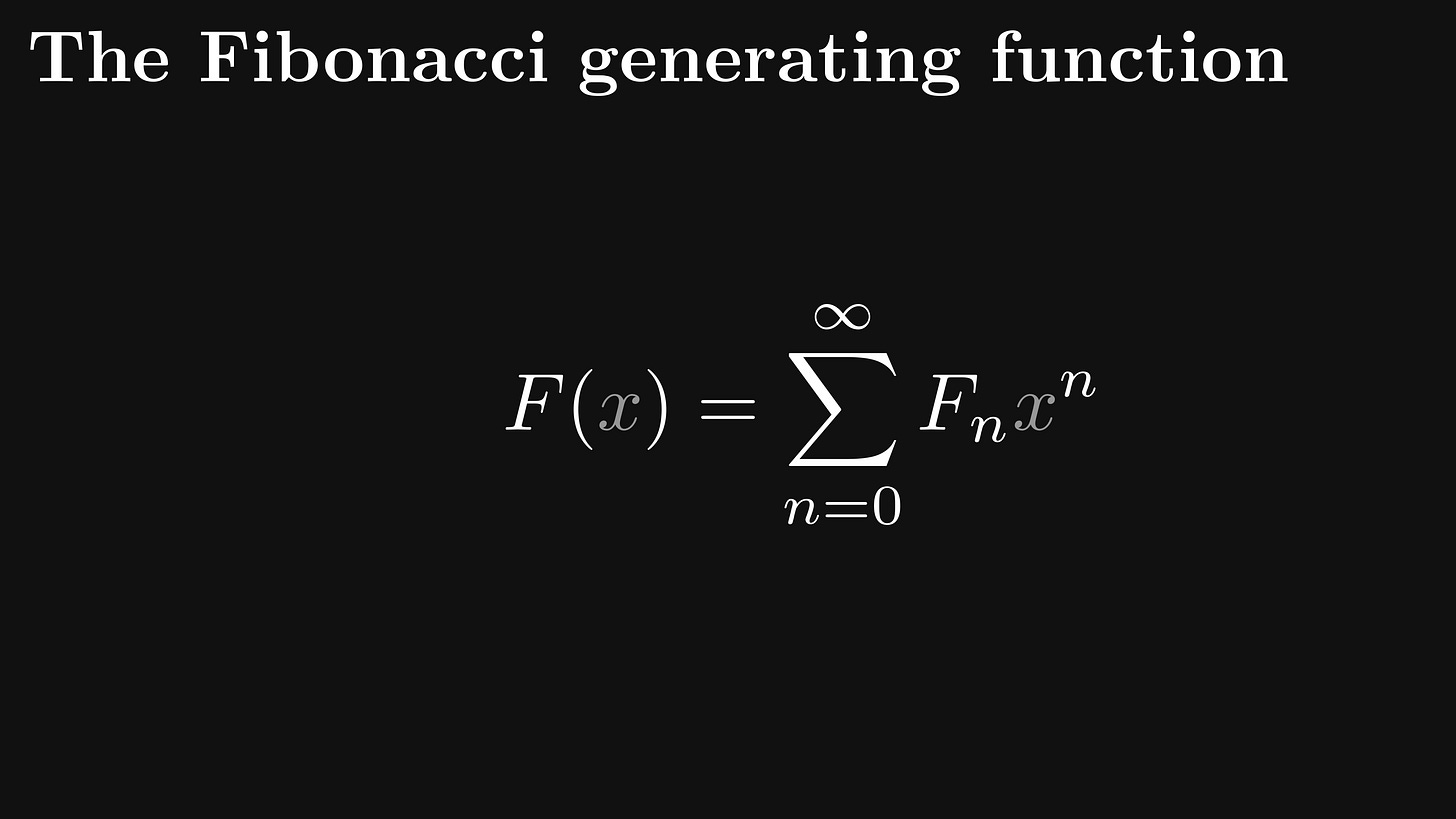
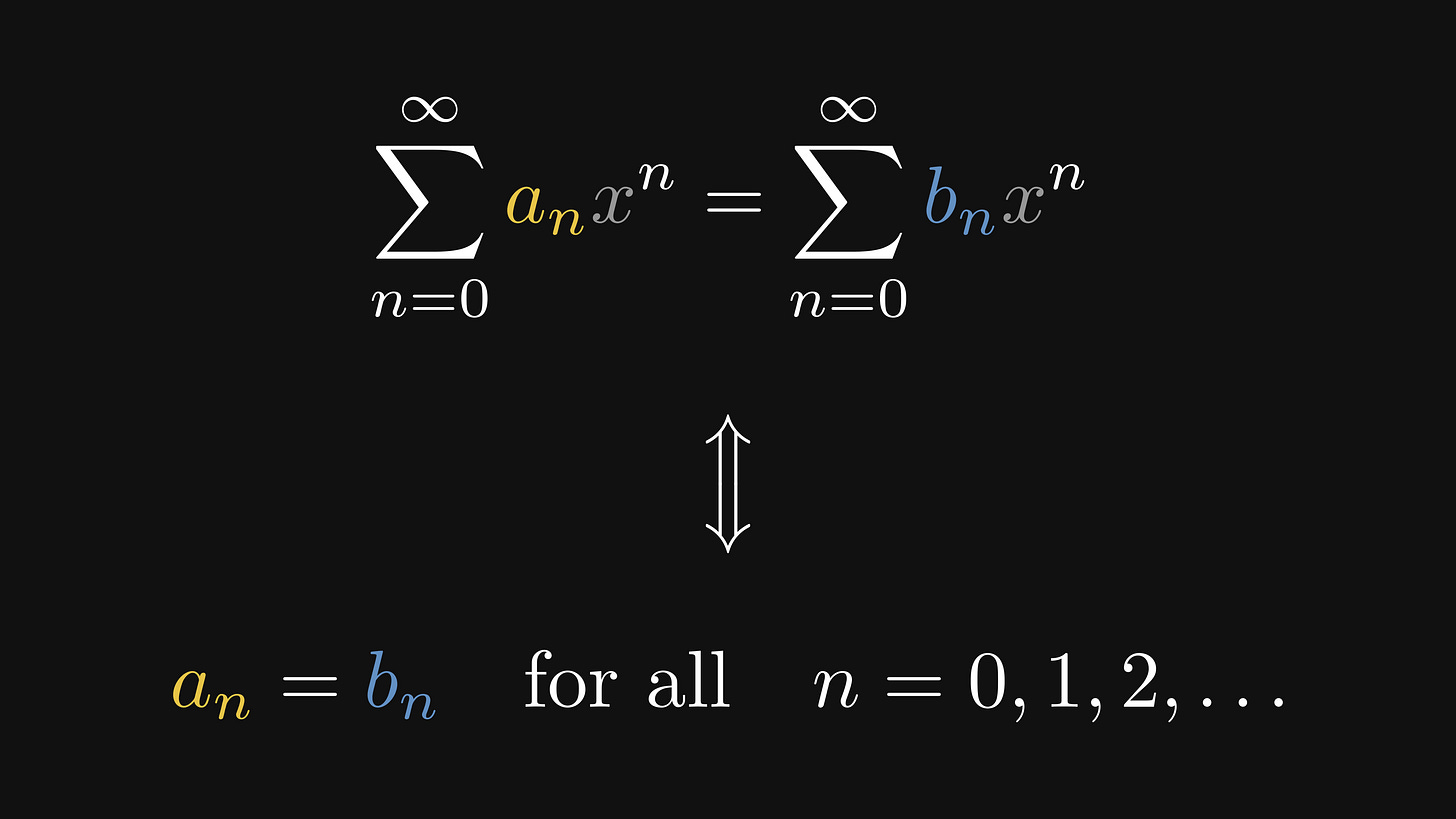
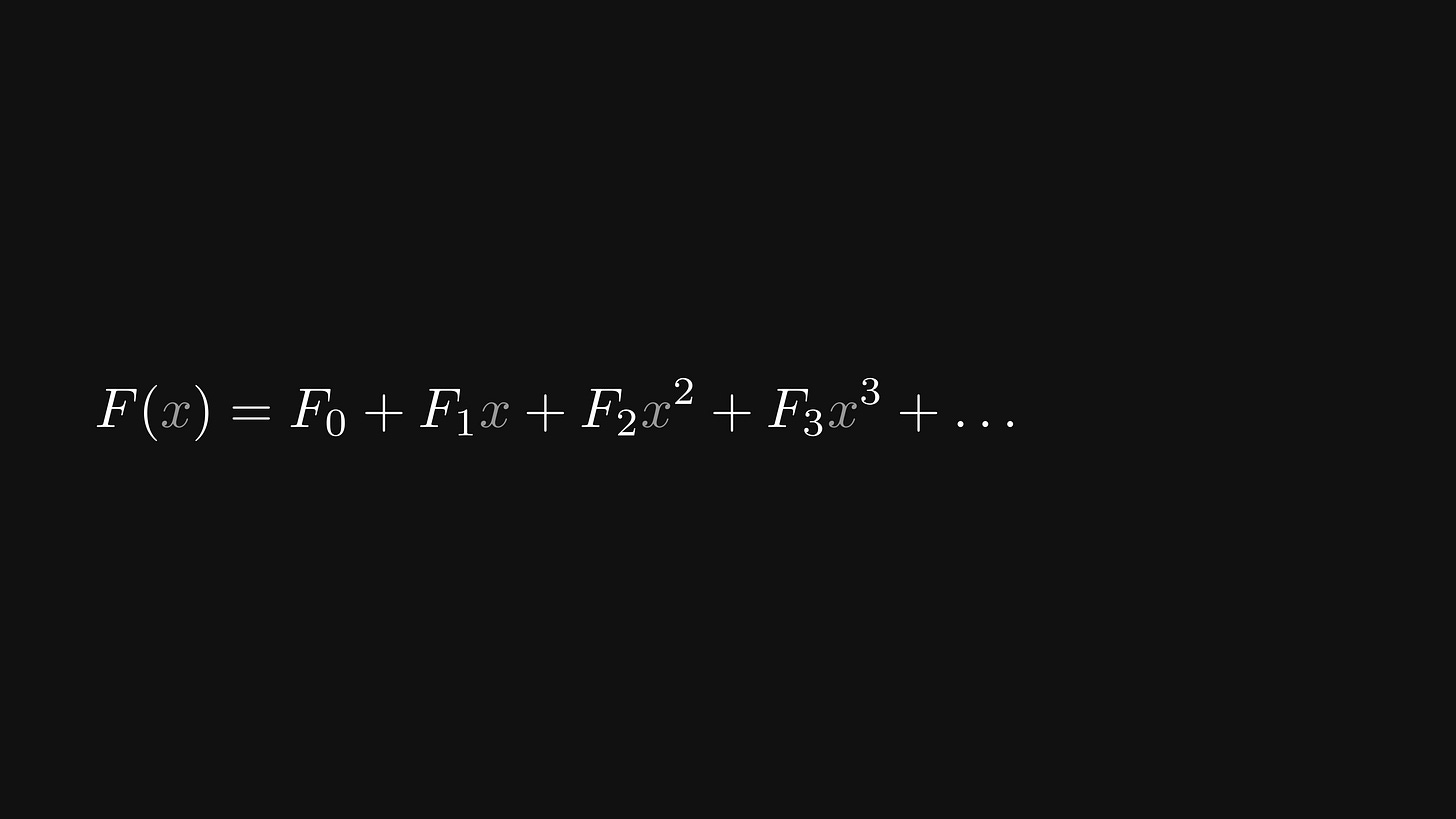
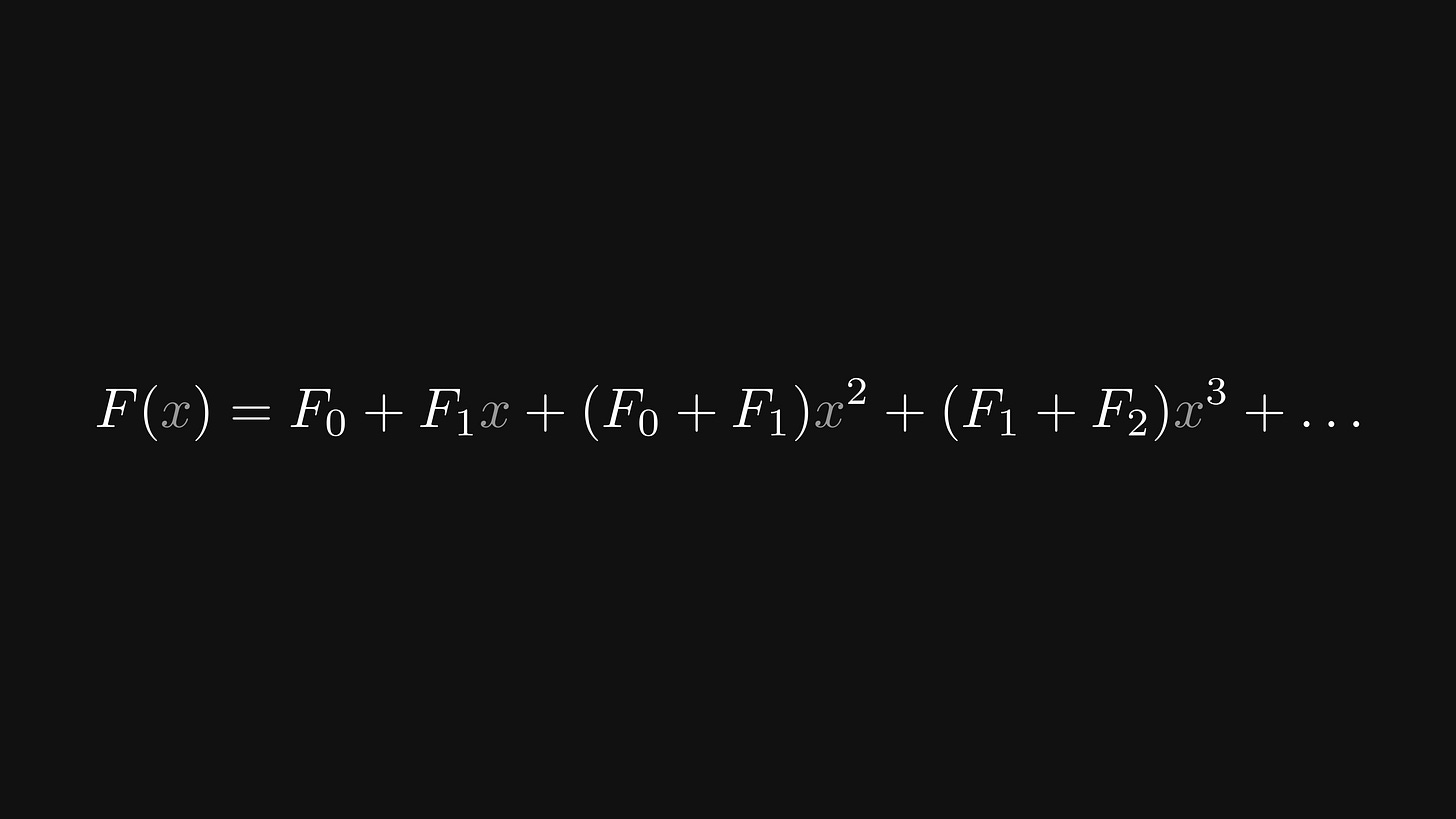
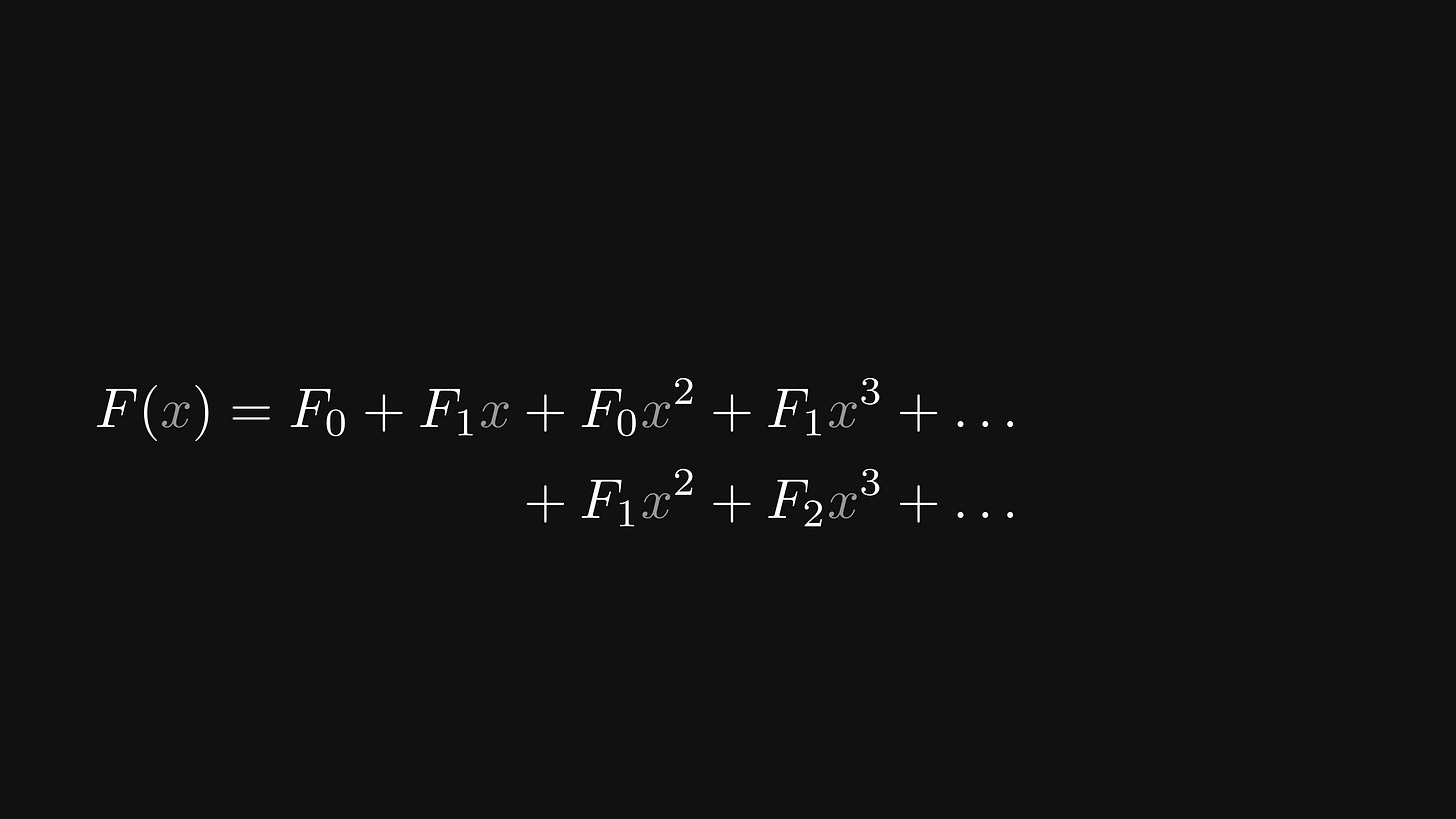
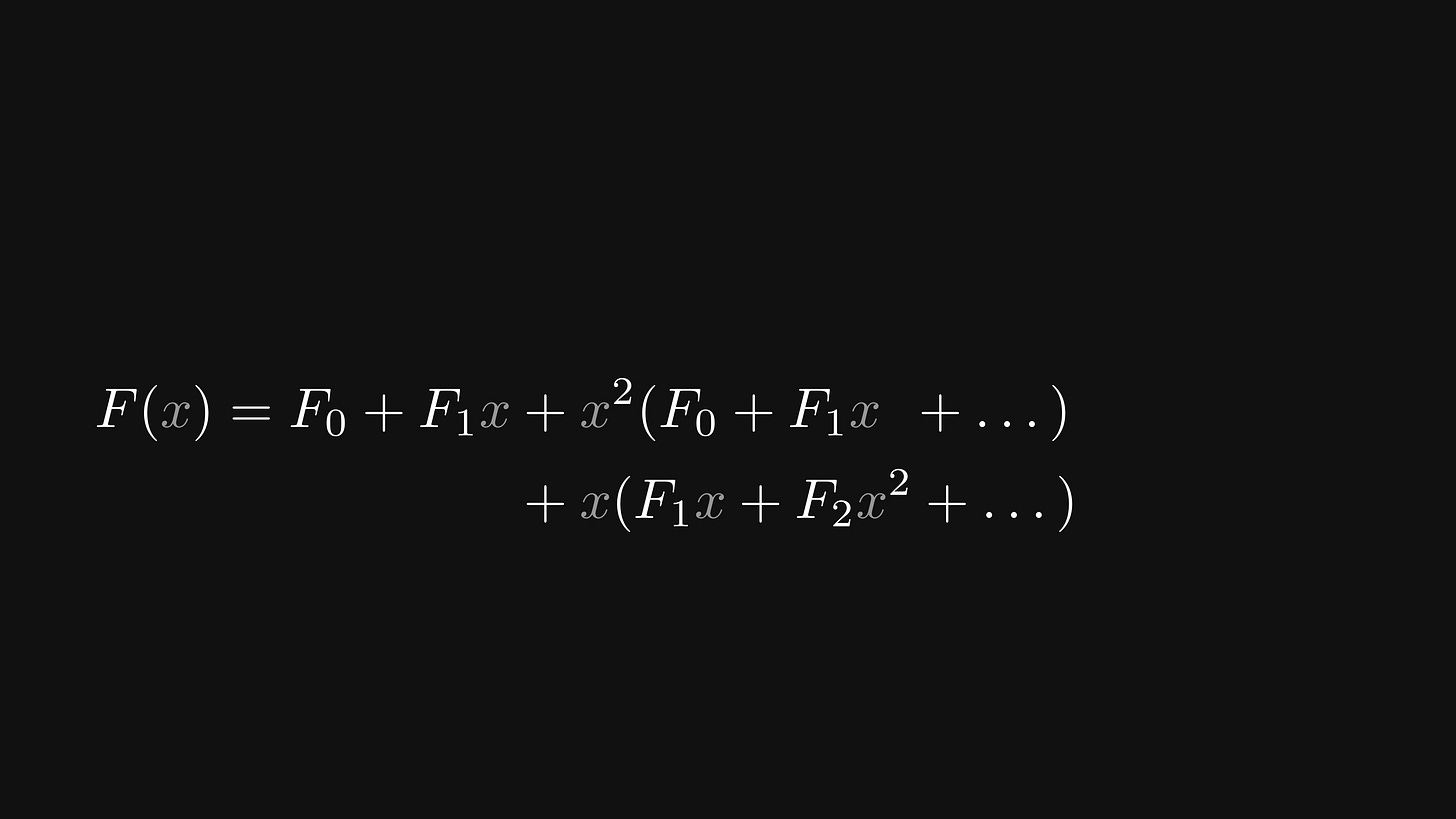
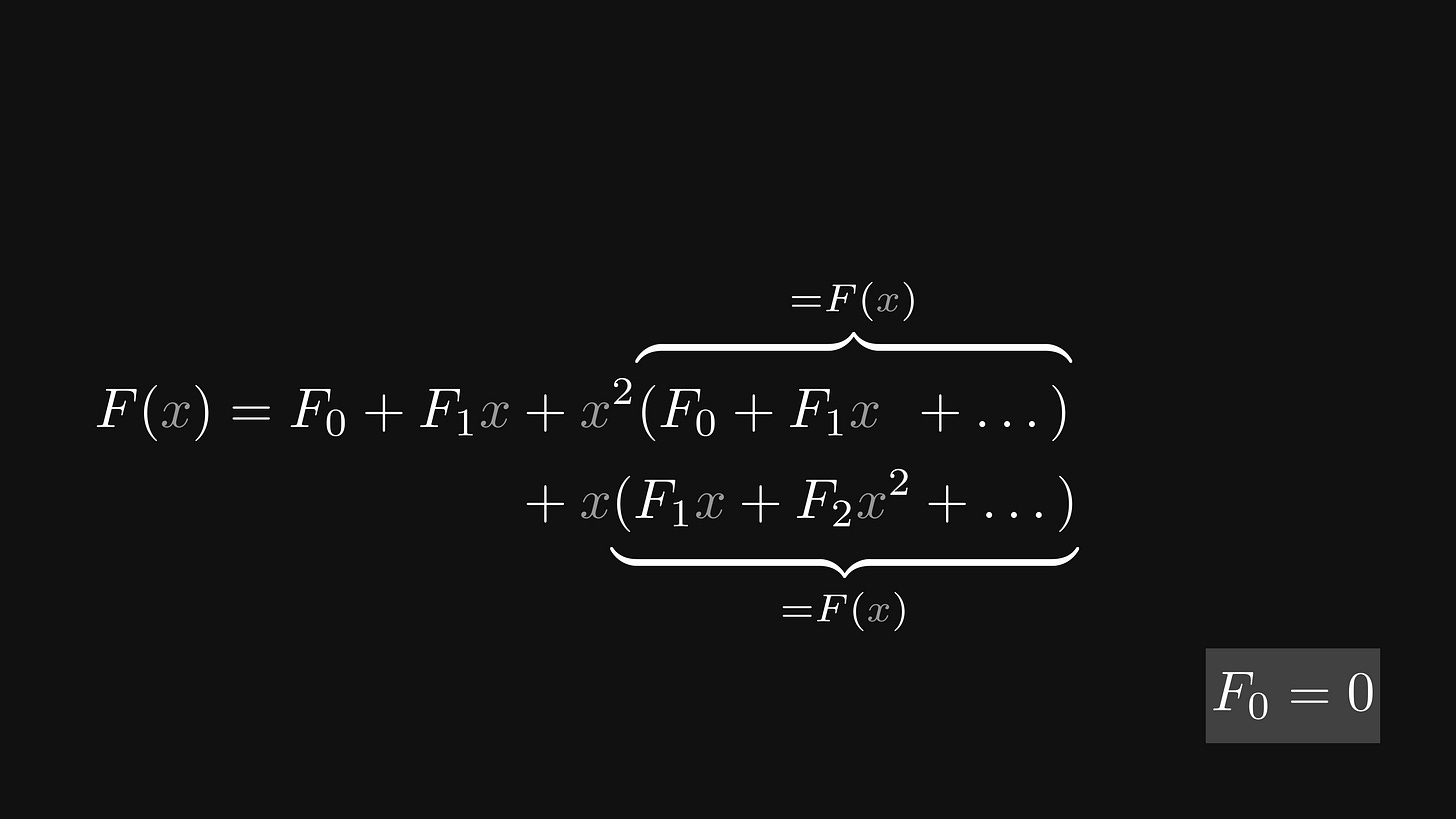
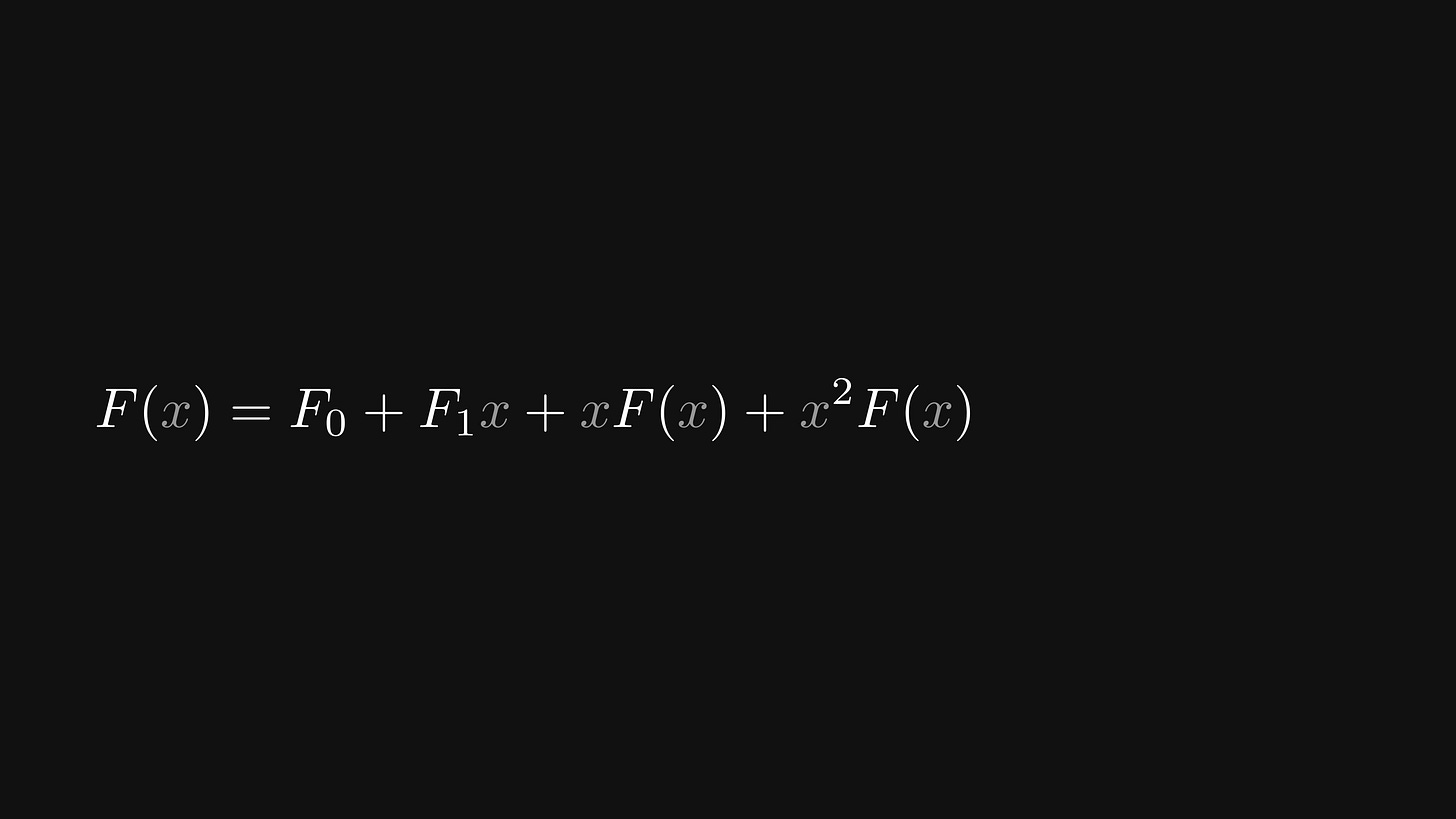
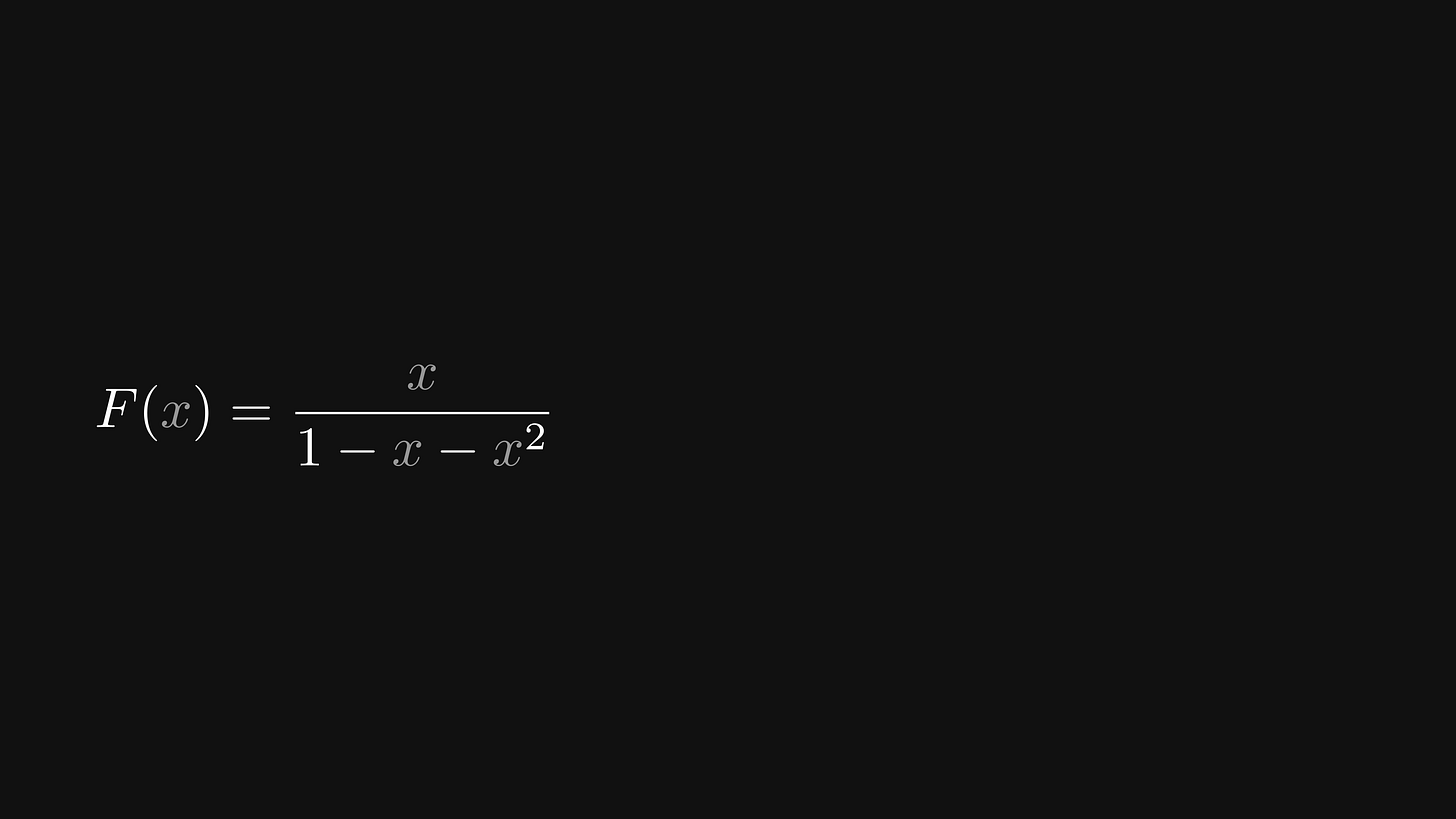

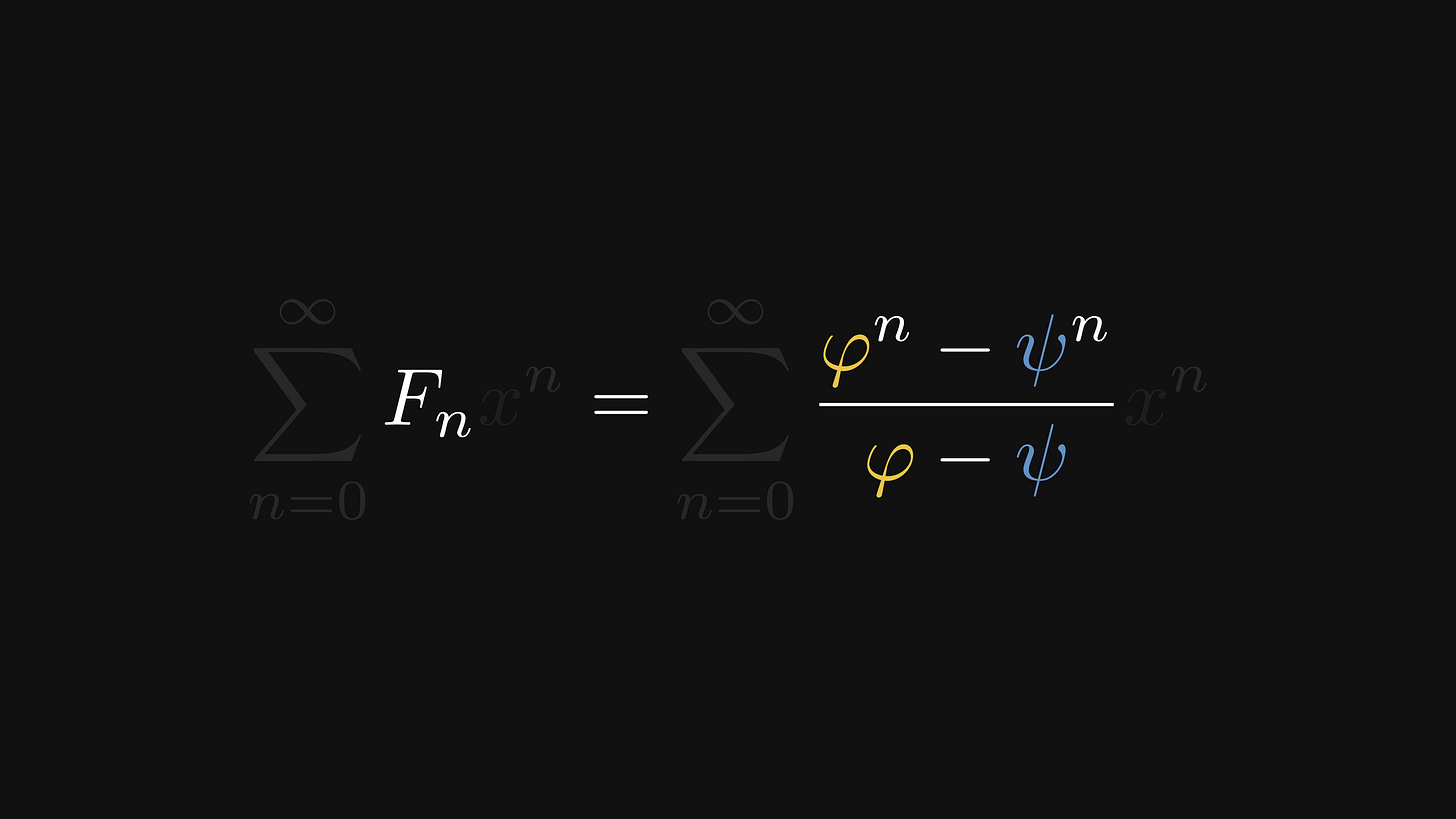

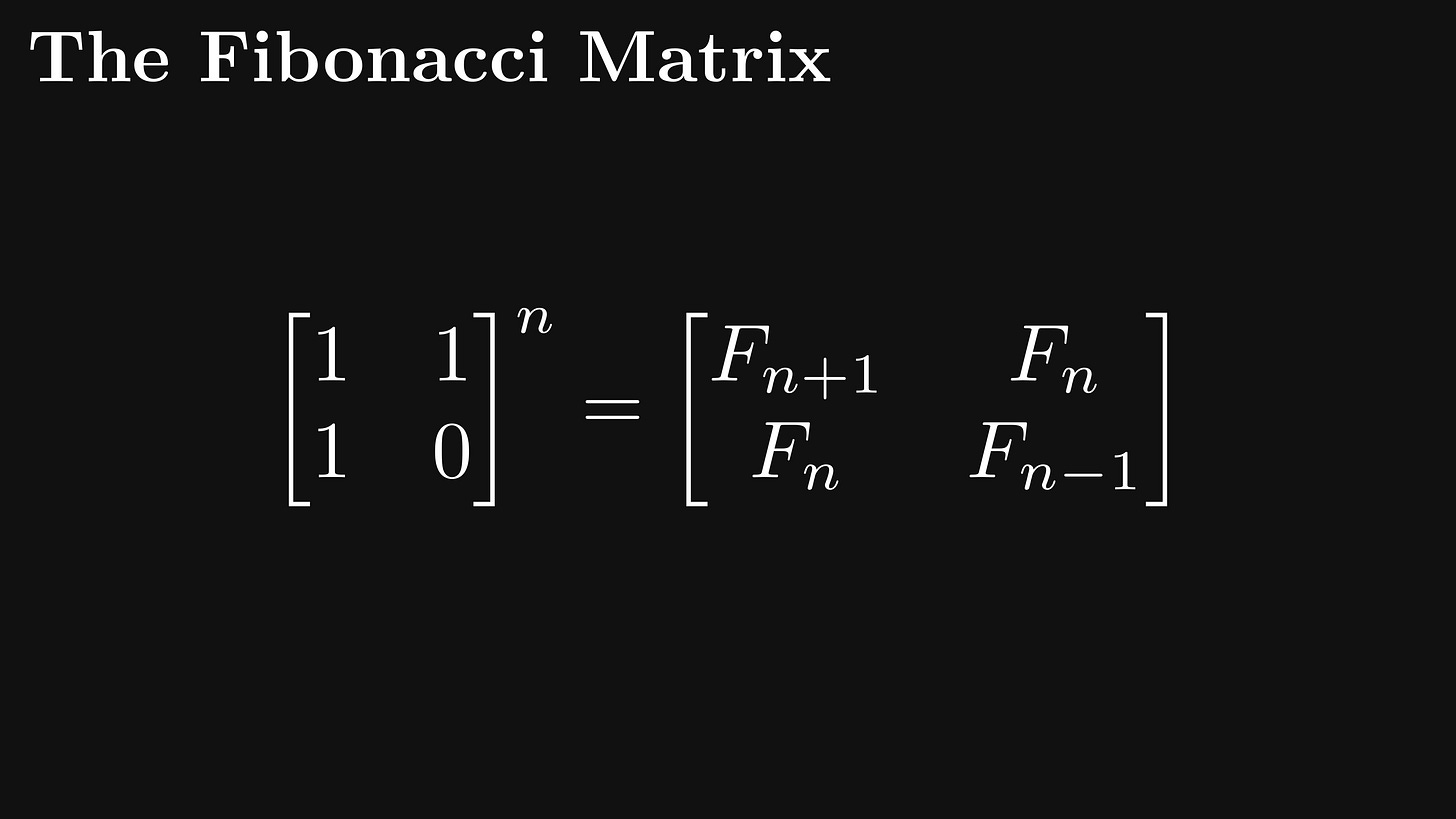
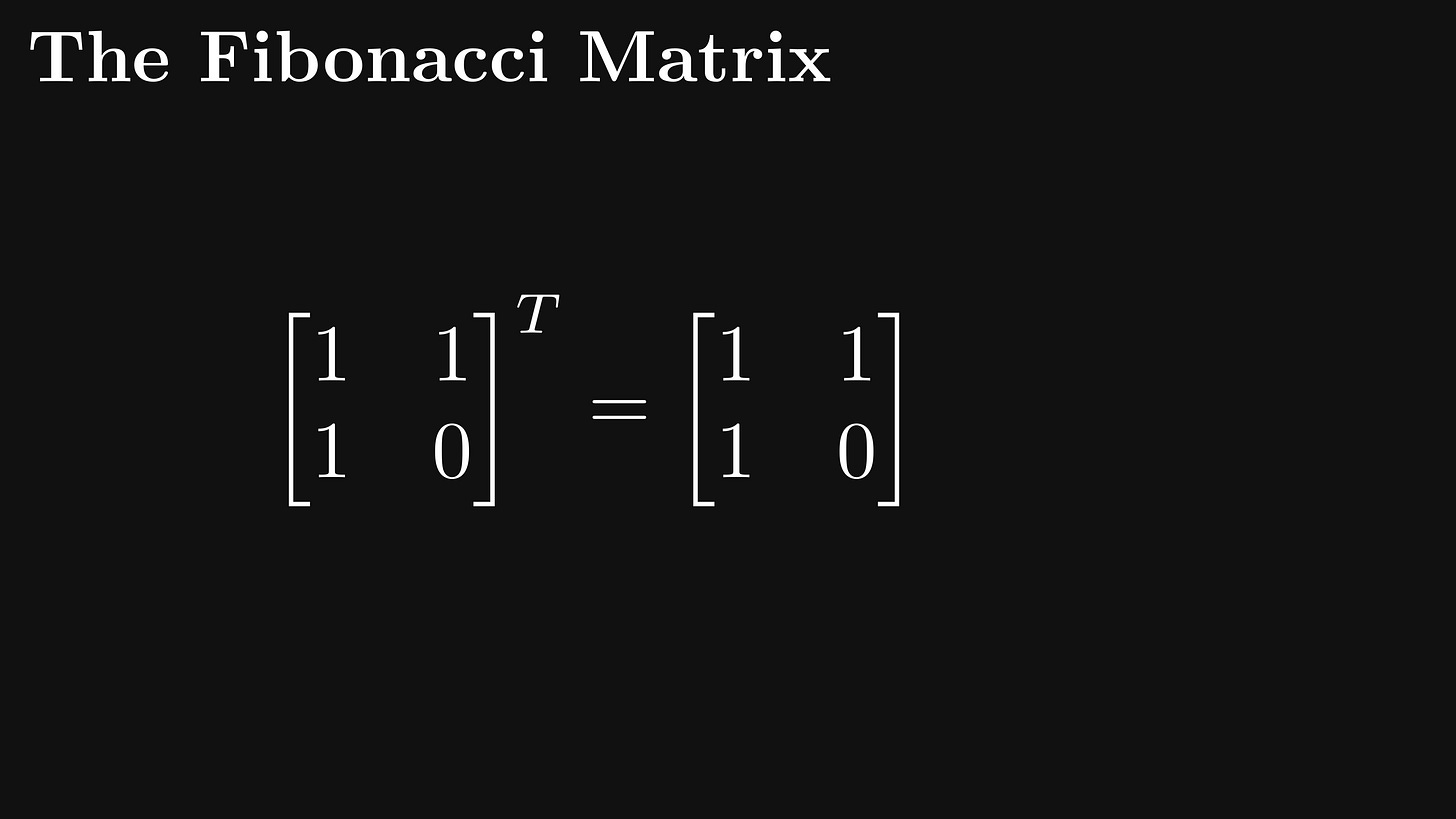
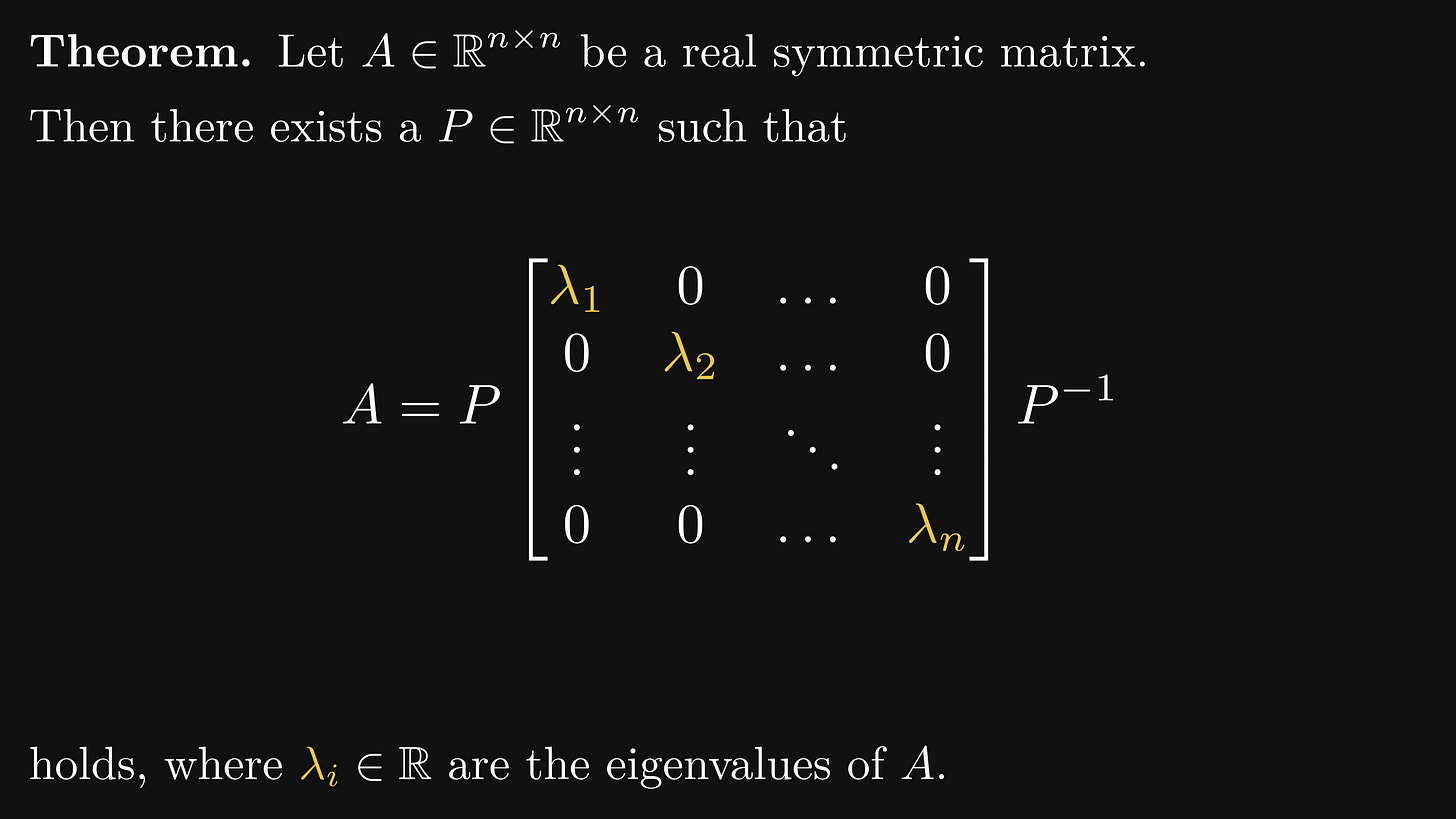
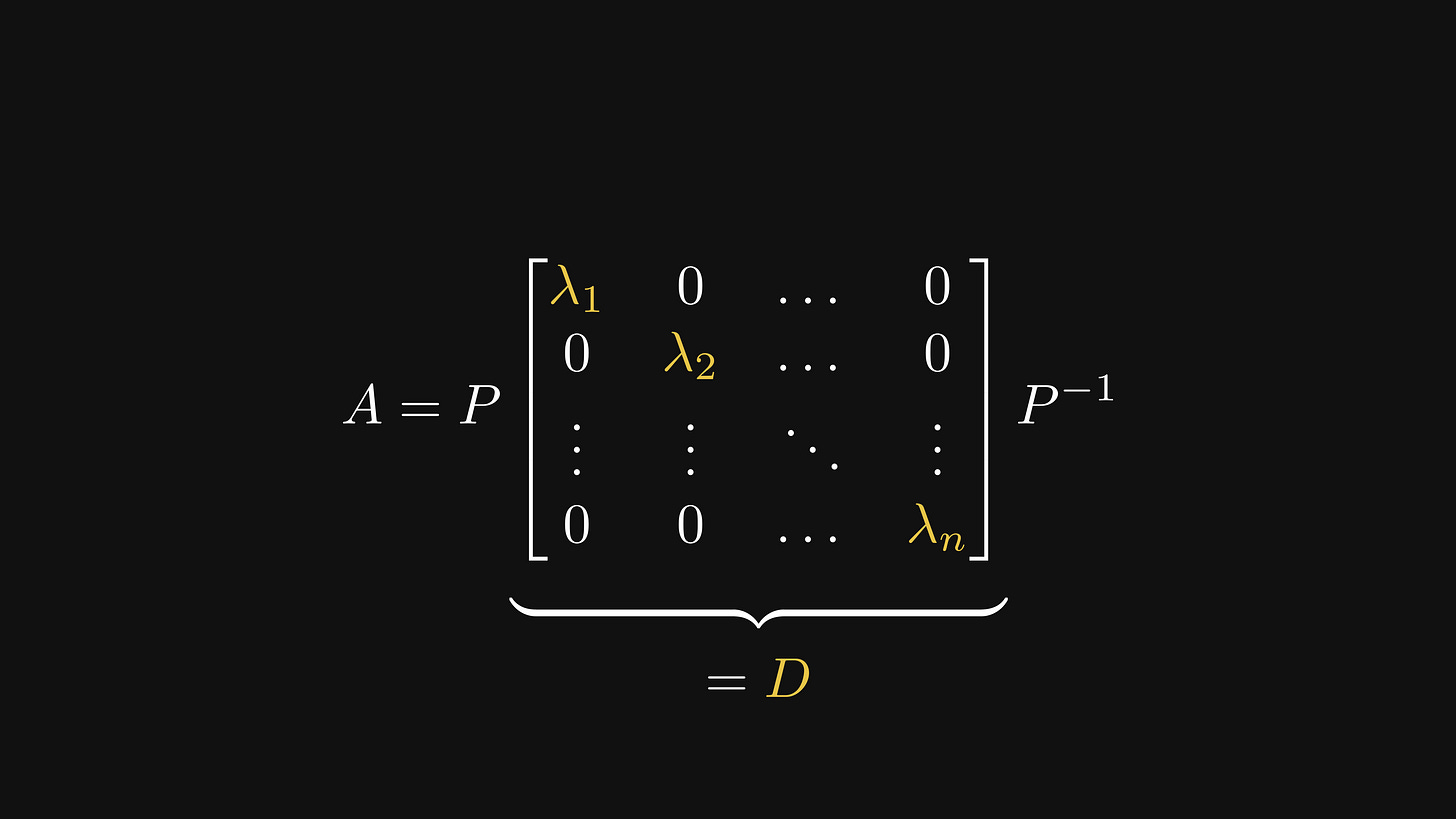
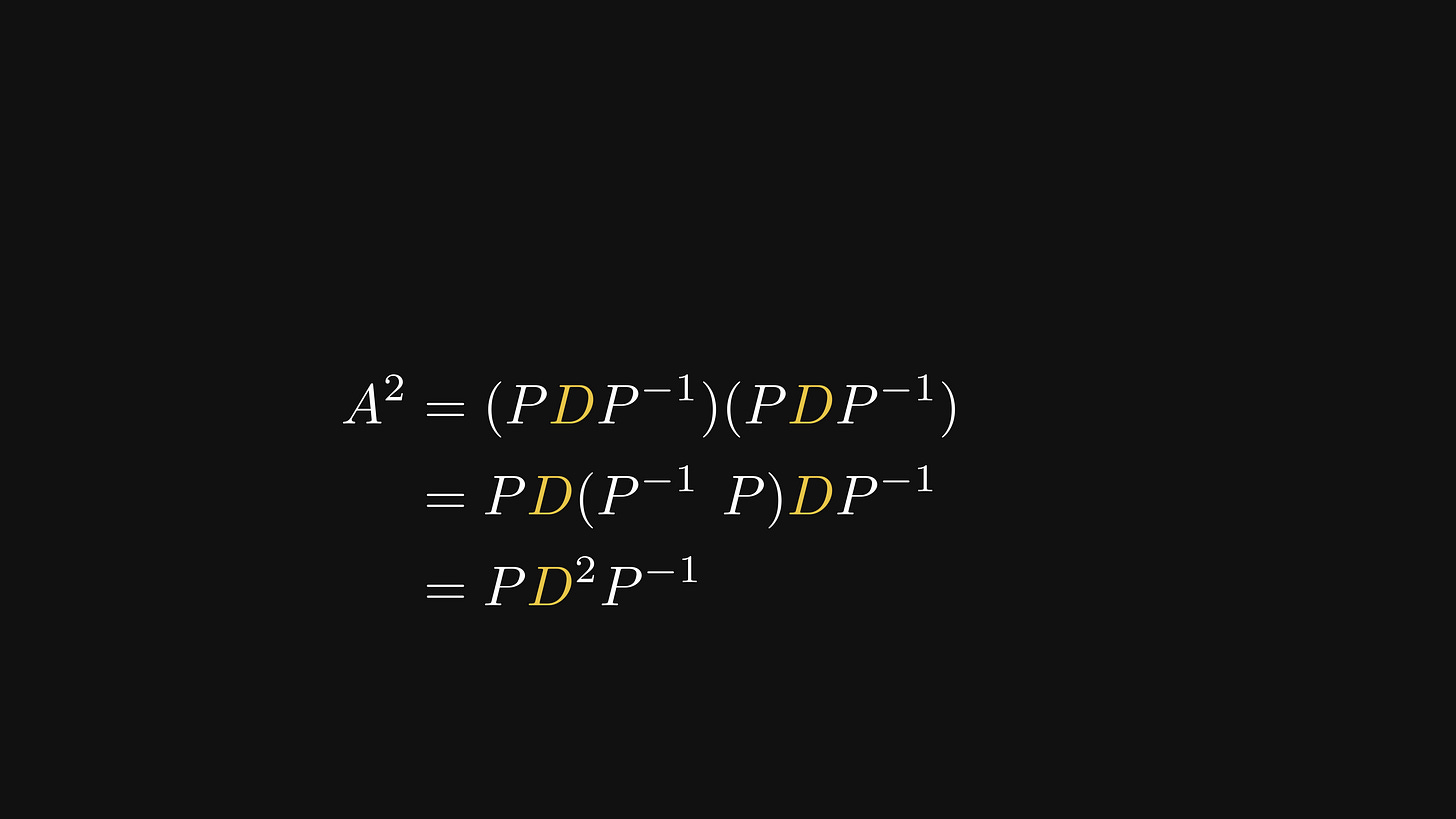
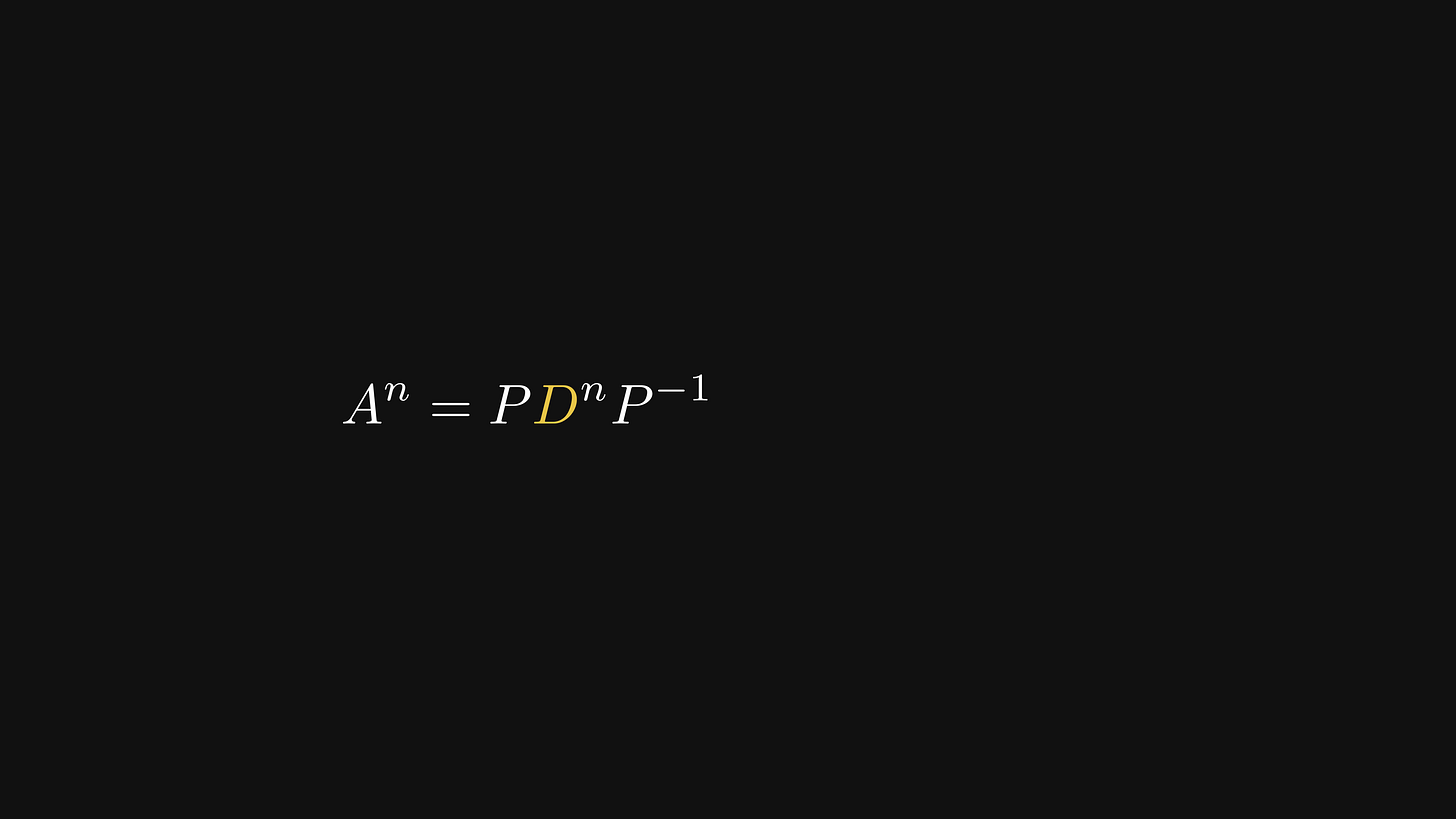
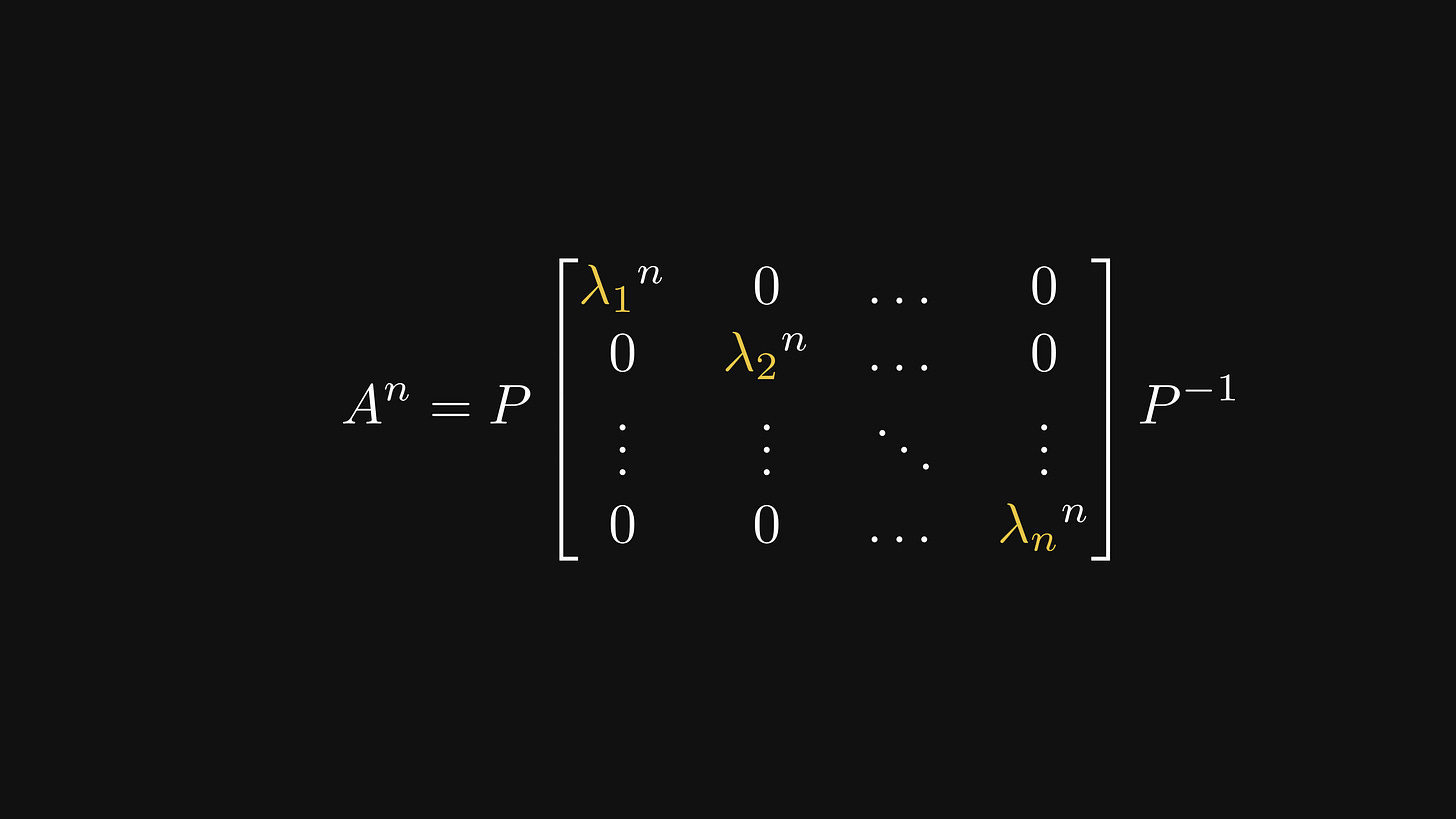
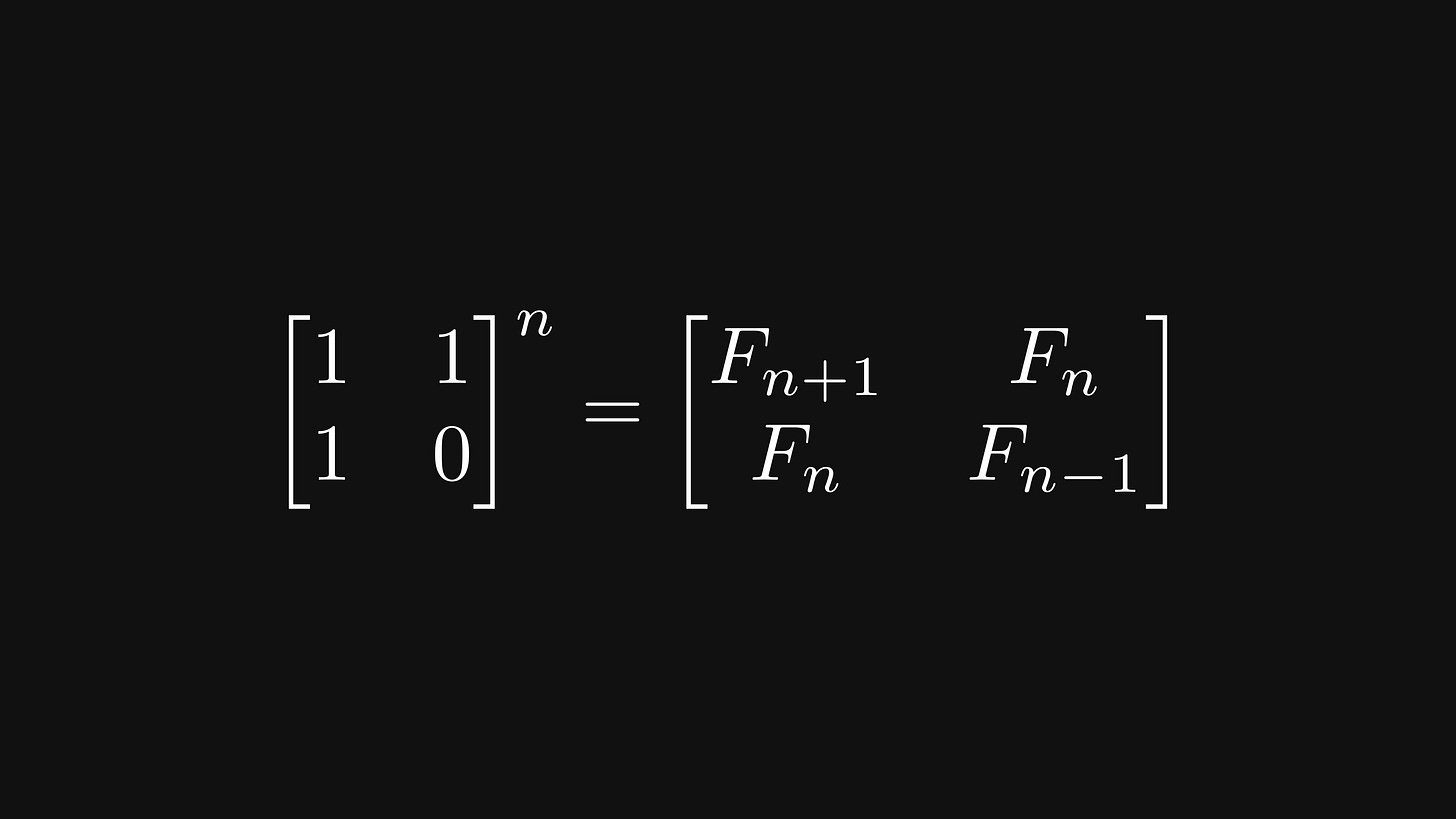
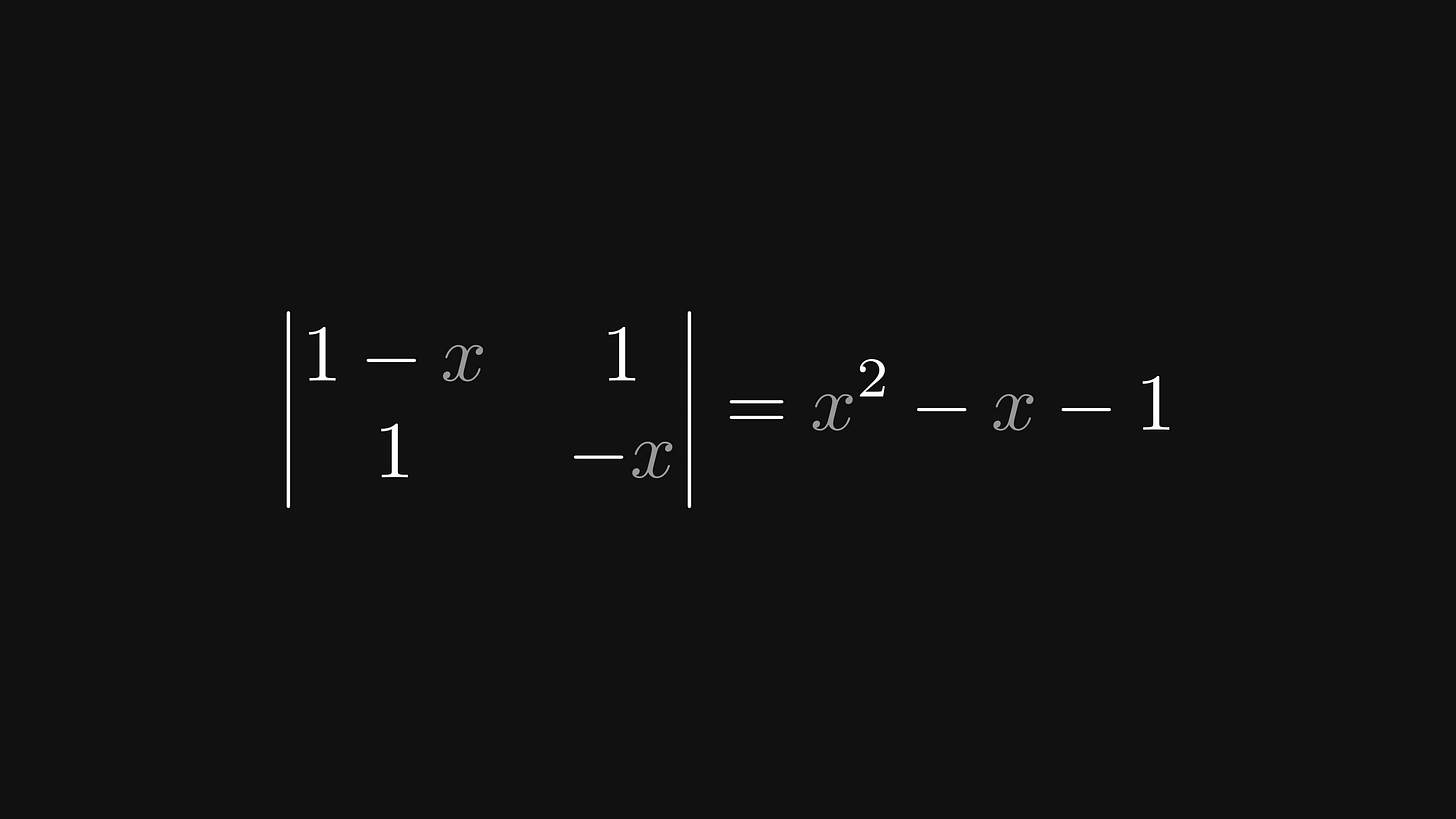
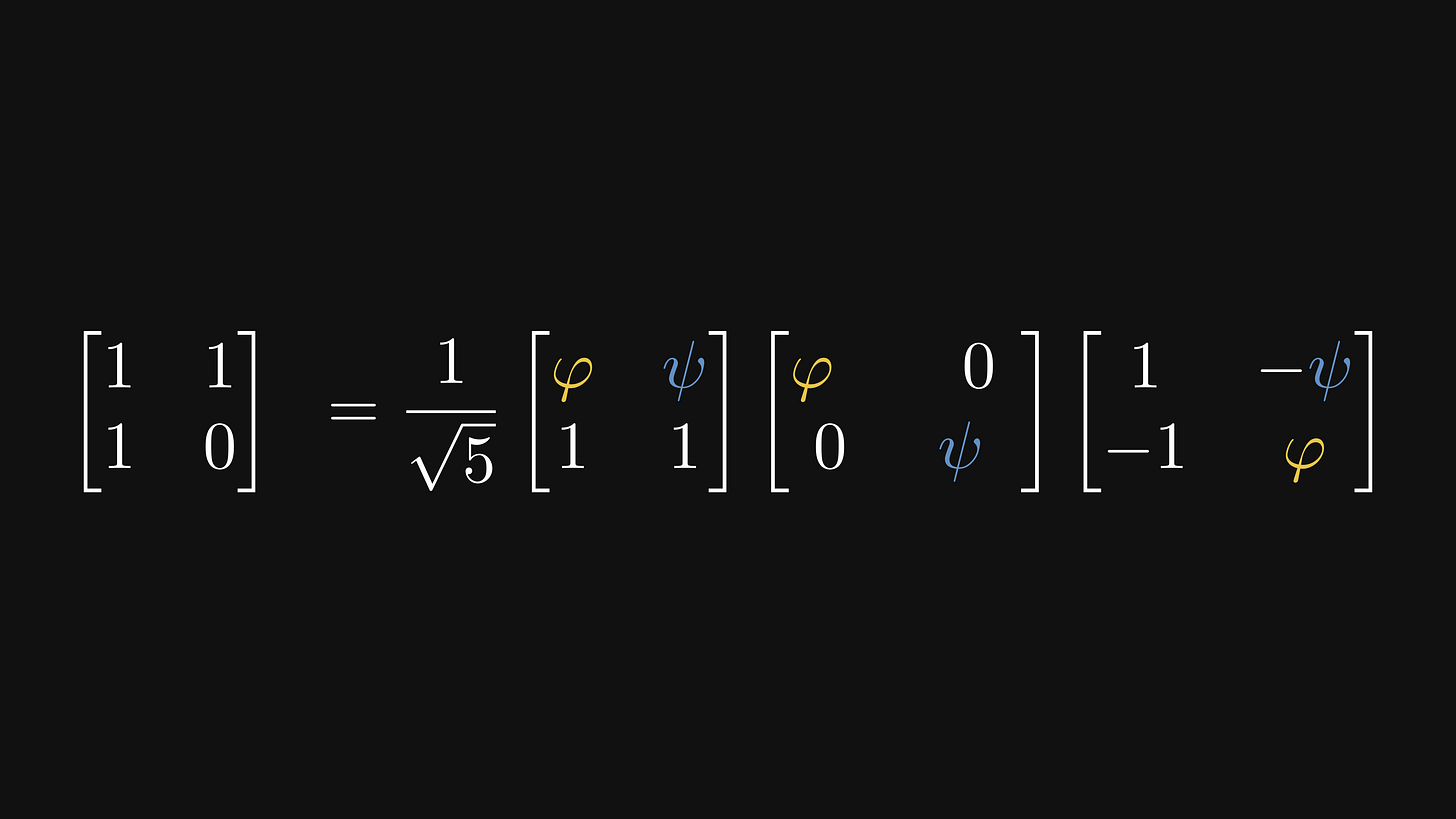
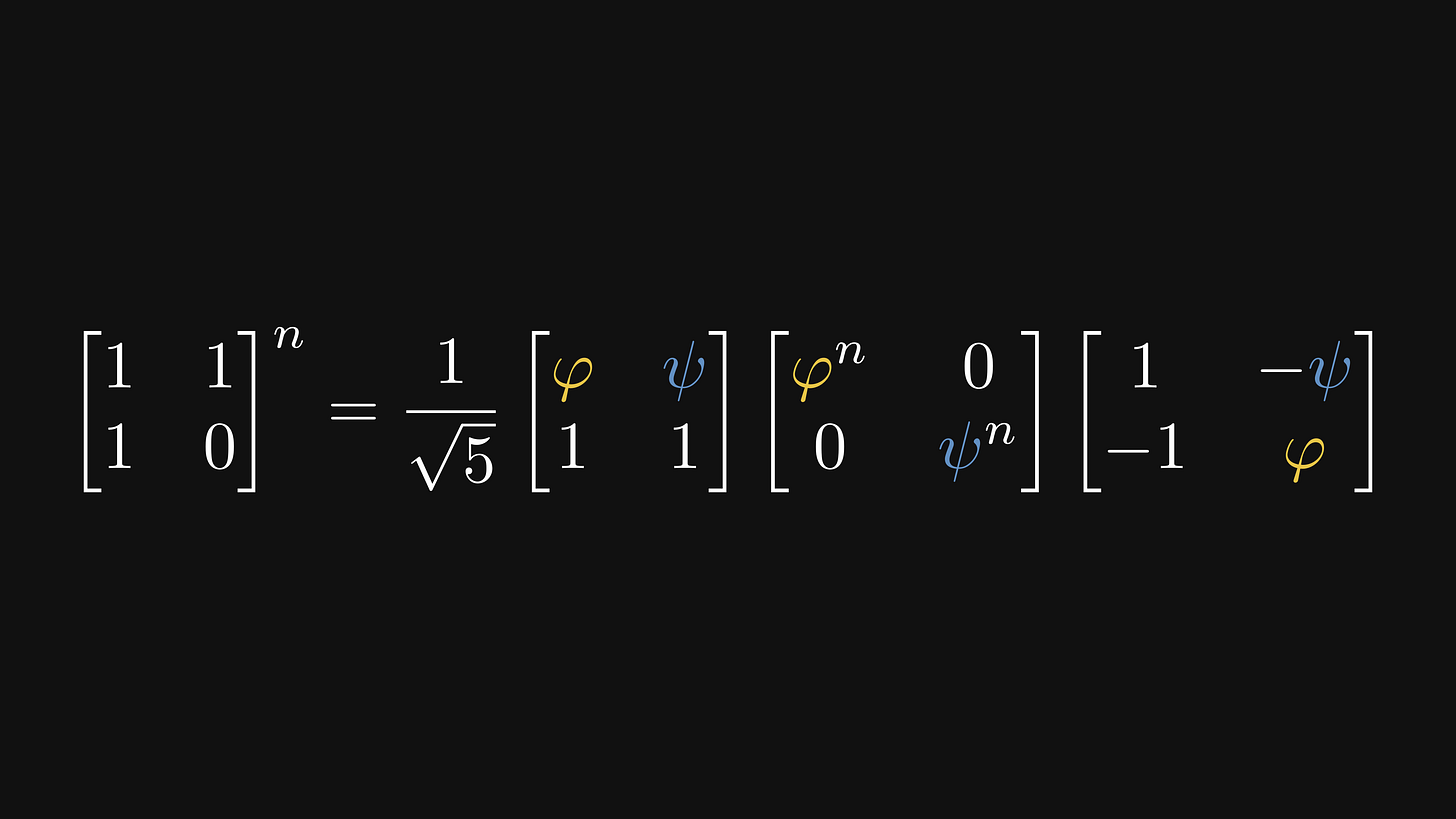
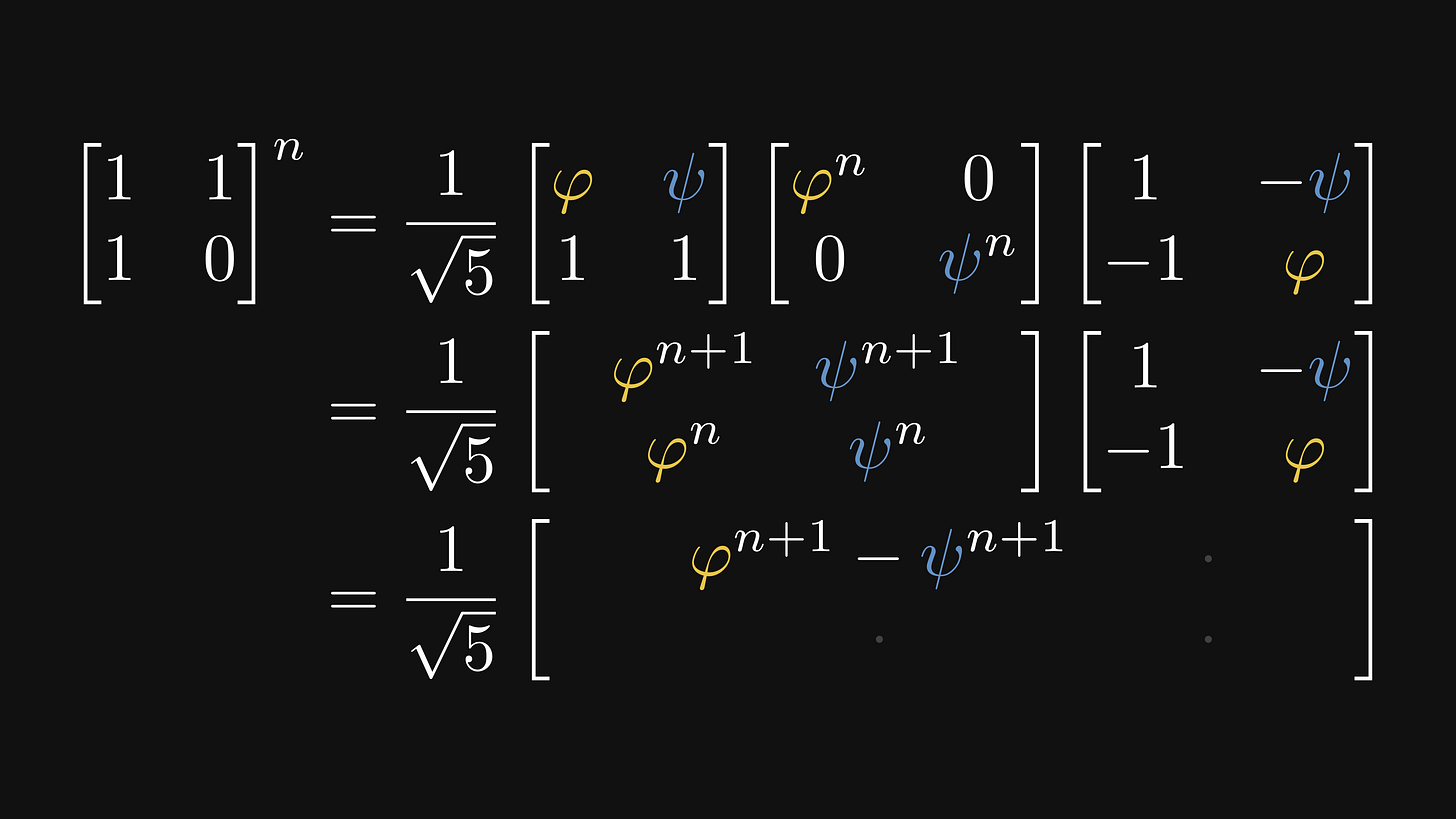
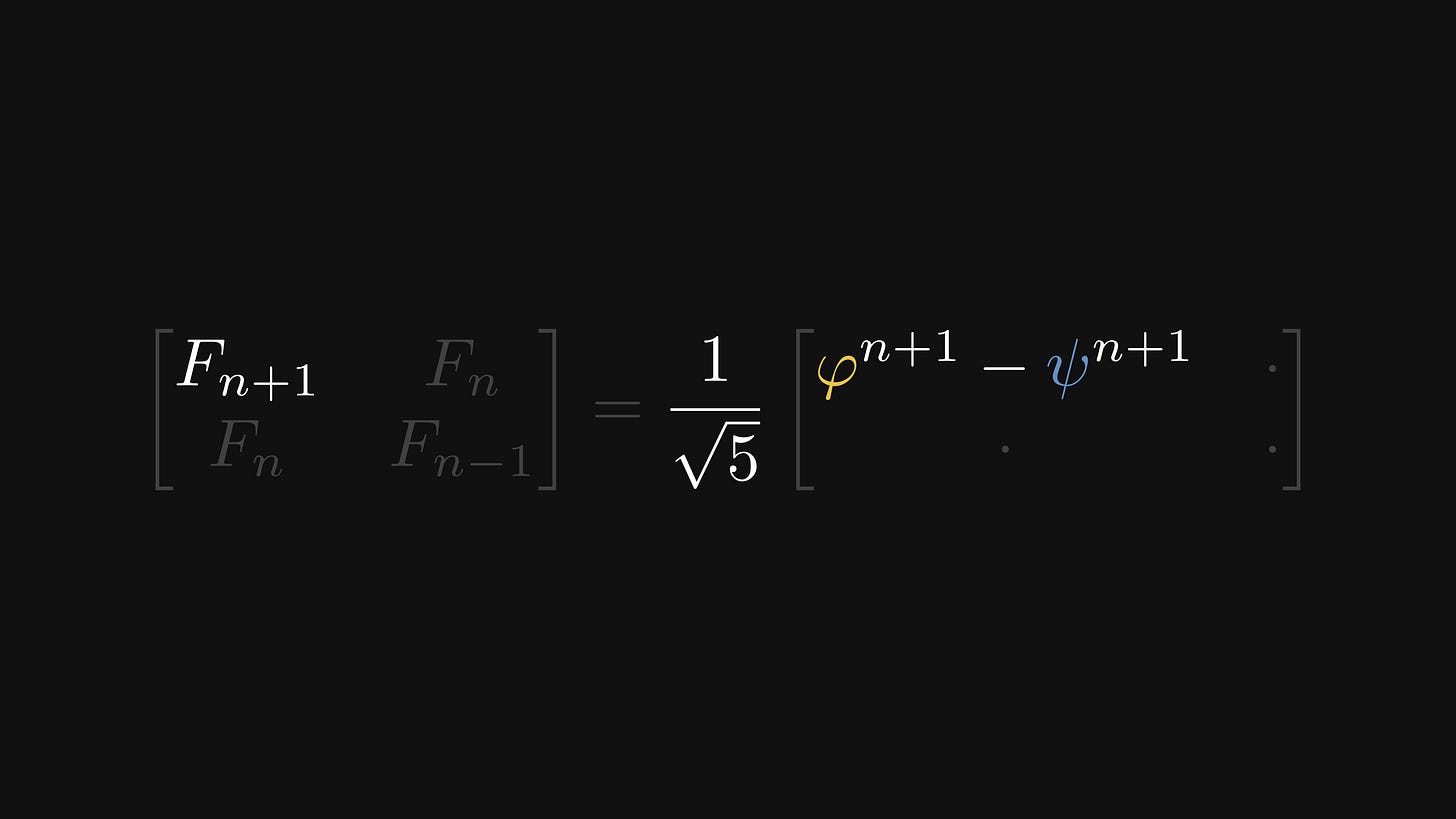


Love it. Saved. Will read it later.
Nice. A good puzzle to play with, as all mathematics is, play with symbols :)