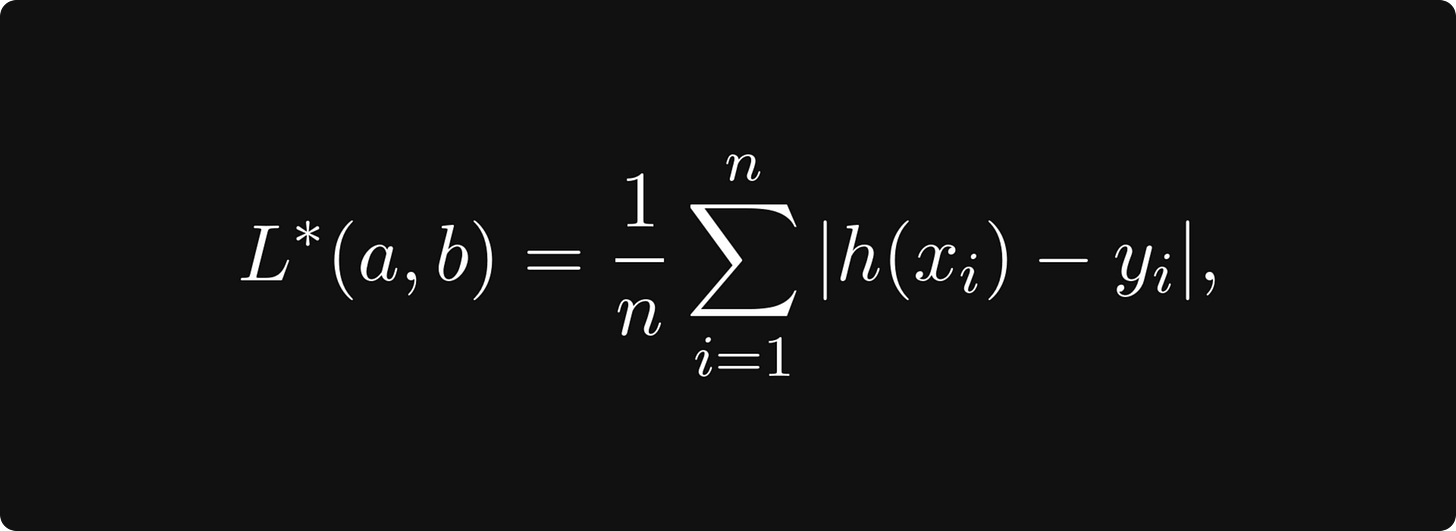Where does the mean squared error come from?

Understanding the most important loss function from a statistical perspective

This post is the next chapter of my upcoming Mathematics of Machine Learning book, available in early access.

New chapters are available for the premium subscribers of The Palindrome as well, but there are 40+ chapters (~450 pages) available exclusively for members of the early access.

---

(Note: this post is a direct continuation of the first and the second post about linear regression, so be sure to check those if you are getting lost in the details.)

If you are an intuitive thinker, you probably feel that we never explained *why* we choose the mean-squared error as the loss function.

Sure, it's mathematically simple and neat, but so is

where |h(xᵢ) - yᵢ| represents the actual distance between the prediction and the observation, not its transformed version.

One reason is that the absolute value function is not differentiable at zero, but there is another explanation: the linear model and the mean-squared error arises naturally when we assume a statistical mindset.

Take one more look at our toy dataset. Can a function adequately explain our data?

No, because for each given input variable x, our observation clearly has a visible amount of variance.

What can we do?