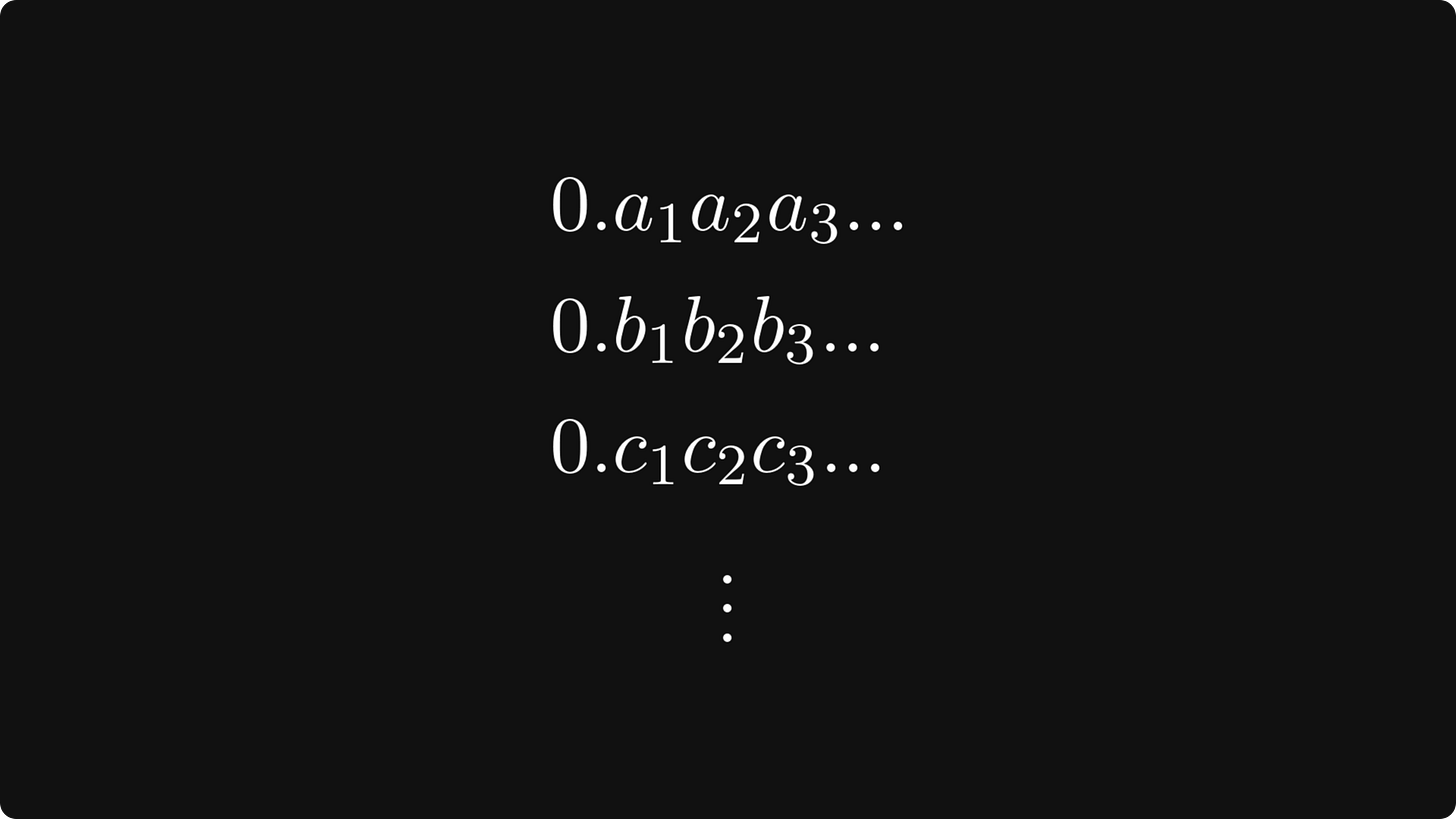What is infinity and how many of them are there?

How infinity broke mathematics

Well, I am glad you asked. Infinity is one of the most mind-boggling concepts that has ever existed. For centuries, infinity has puzzled great thinkers across all disciplines.

The first people to finally tame it were mathematicians, but this came at a cost. In this post, I would like to tell you the story of infinity and how it made things infinitely more complicated in mathematics.

What is finite?

To understand infinity, let’s start small. Suppose we are talking about quantities. I have infinite problems. Great scientists have infinite ideas. Jeff Bezos has an infinite amount of money. These are just figures of speech, so let’s put the math behind the idea.

First, let’s assume that the objects we are counting are elements of a set. From now on, we call the measure “number of elements in a set” the cardinality of the set. Mathematically, the cardinality of a set is denoted by writing the set itself in between absolute value signs: |A|.

What is it that we need to know about counting? Counting may seem like a trivial task, but trust me, it is not. To make things precise, there are three rules of counting.

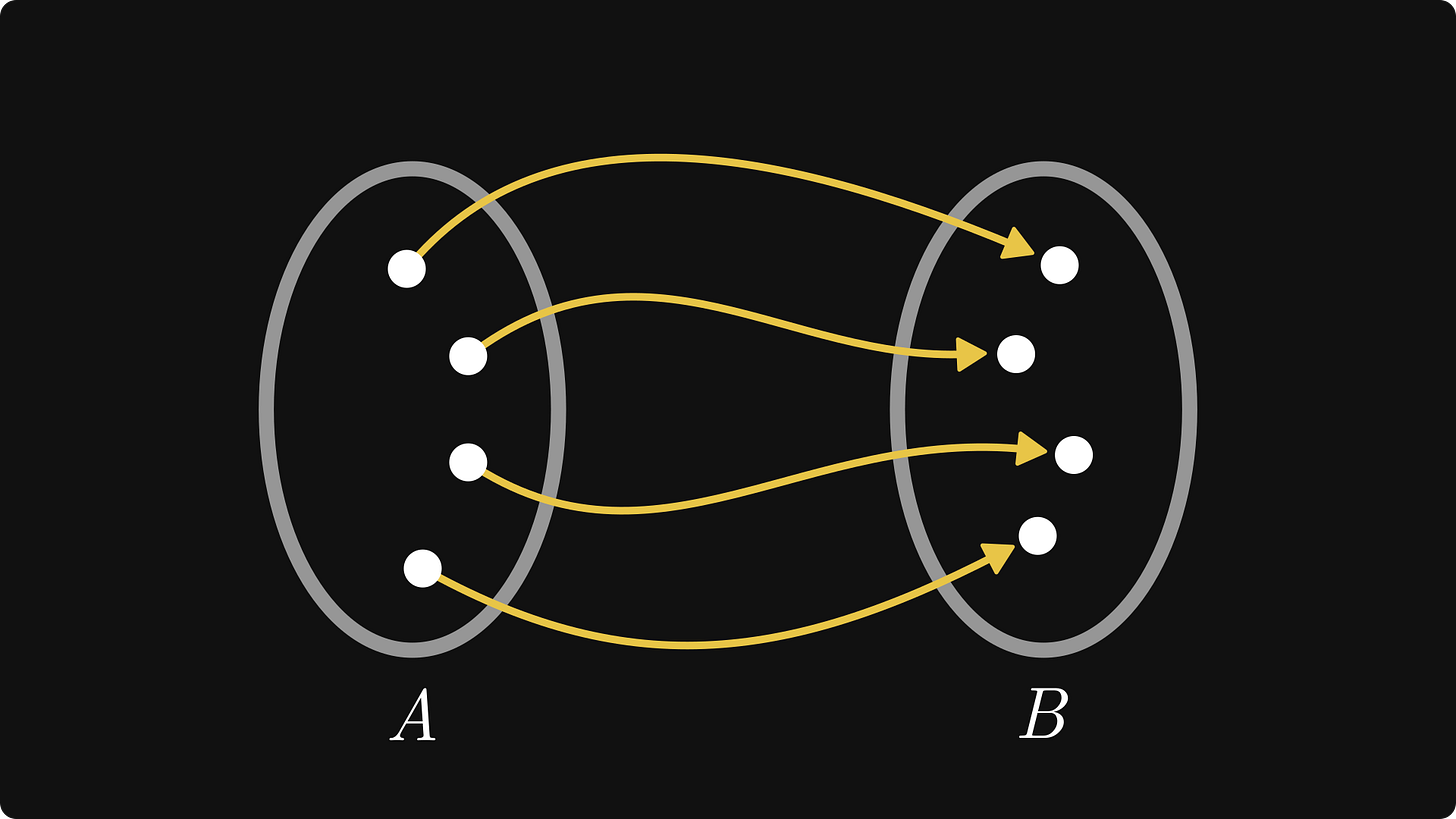
Fundamental rule no. 1. Two sets have the same cardinality if we can pair each element between them. Simple enough. For instance, take a look at this picture below.

There are four riders. Because each rider has exactly one horse, we don’t need to count to know that there are four horses.

To make it a bit more abstract, you can imagine a pairing as drawing arrows between elements of sets, just like below.

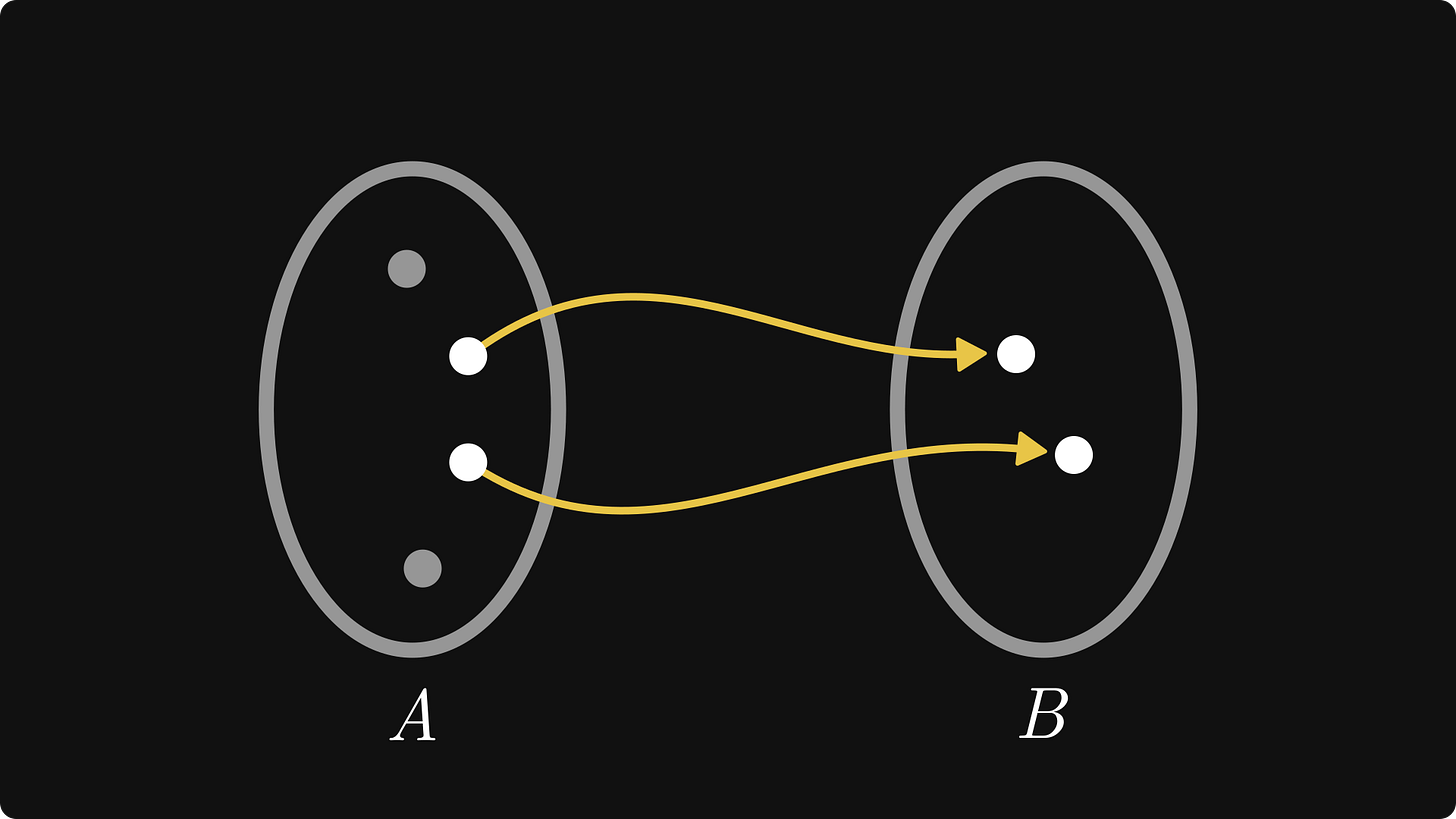
Fundamental rule no. 2. The set A has more elements than the set B when you cannot find pairs for every element of A.

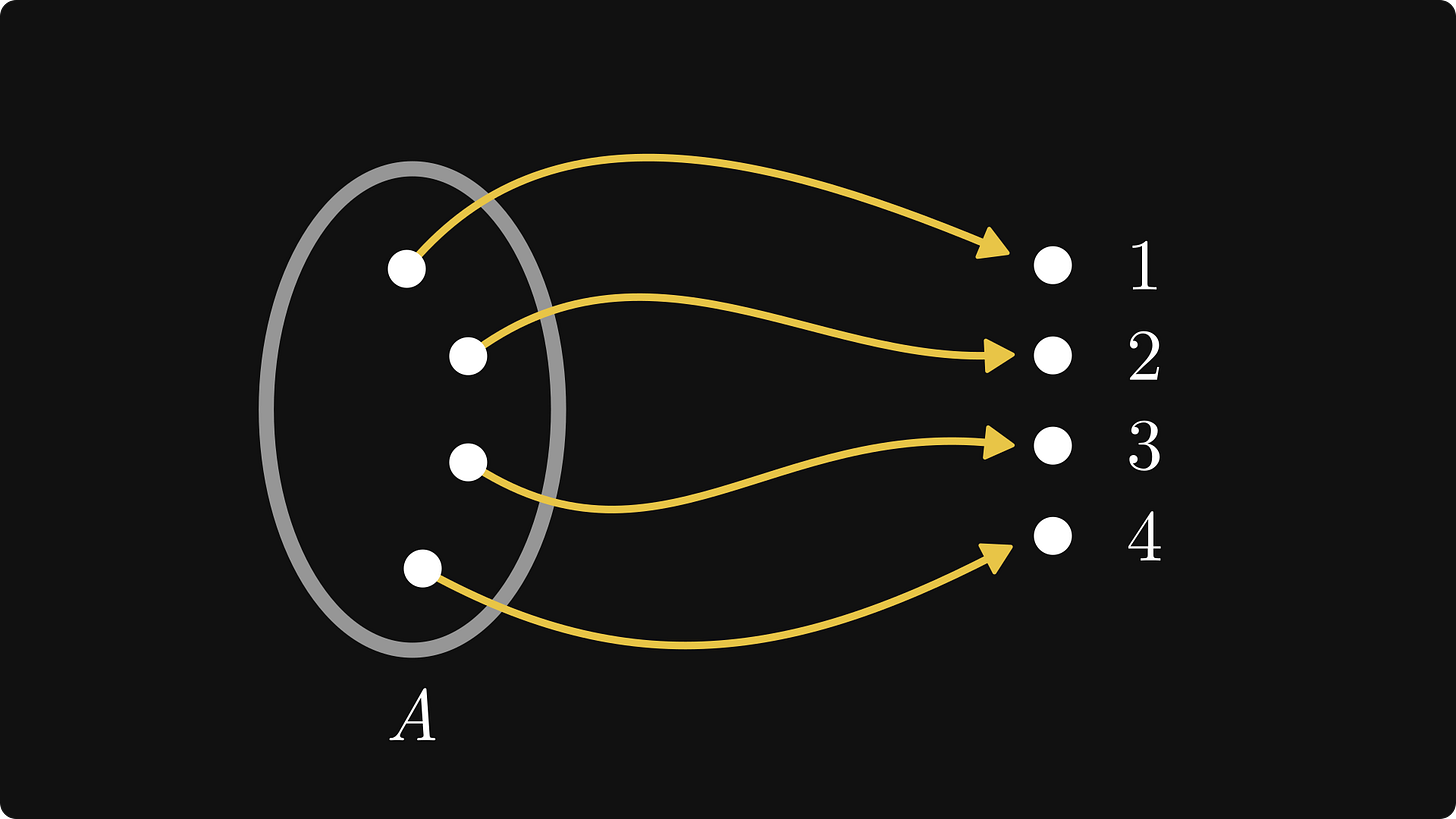
Fundamental rule no. 3. A set is finite and has n elements if you can pair it with the set {1, 2, 3, …, n}, that is, the set of the first n natural numbers. (Fun fact: mathematicians still cannot decide whether zero is natural or not.)

So now we know what finity is. How about we go one step further?

The smallest of infinities

Previously, we have seen that finite sets are finite because they can be paired with specific subsets of natural numbers. Why don’t we do the same for infinity? We say that a set A is countably infinite if there is a pairing between A and the natural numbers.

(For notational simplicity, let’s denote the set of natural numbers as ℕ from now on.)

Let’s see a few examples of countably infinite sets!

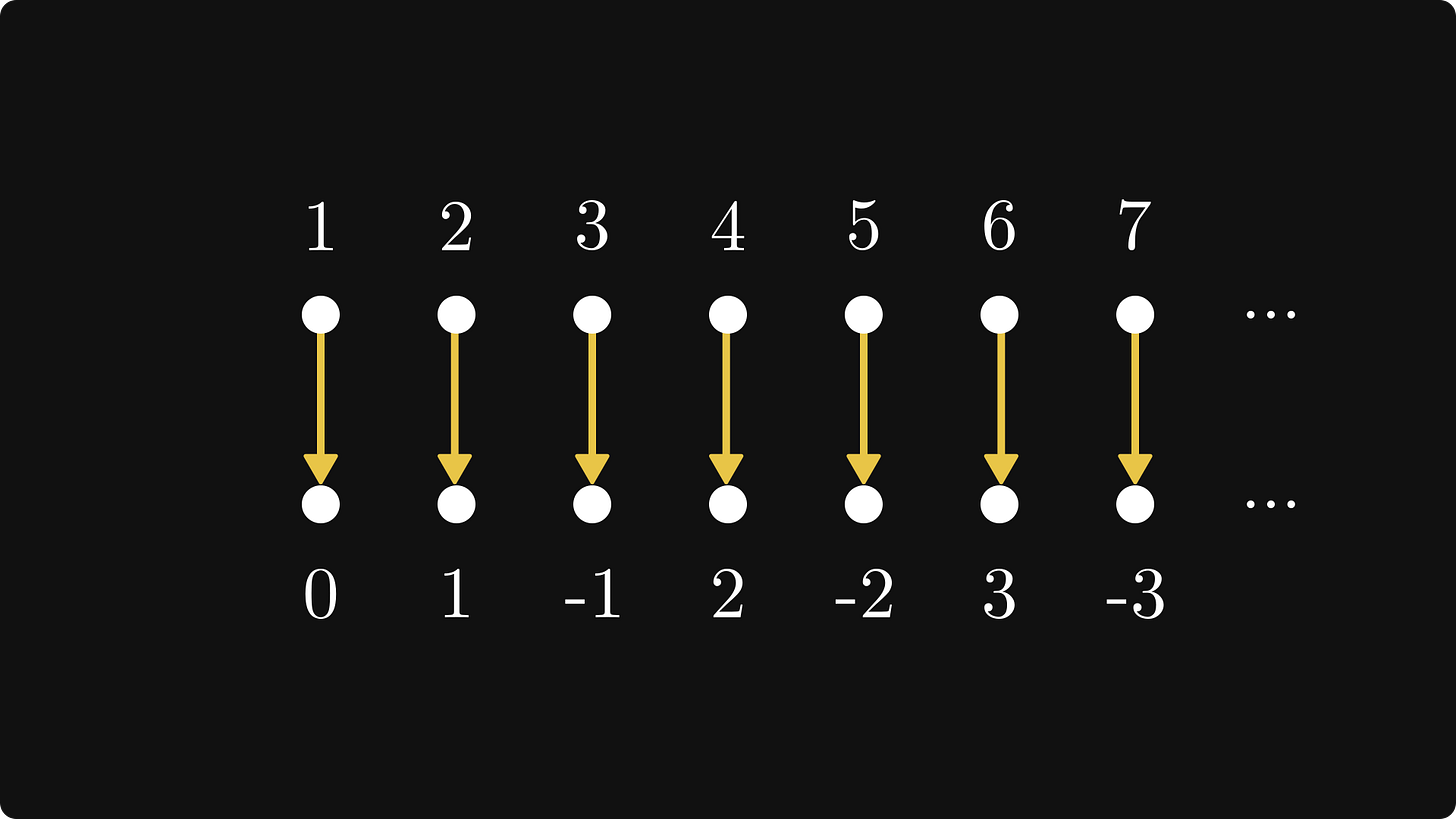
Example 1. The set of integers: ℤ = {…, -2, -1, 0, 1, 2, …}.

This might be counterintuitive at first, because, well, it seems like there are at least two times as many integers! But let’s not forget the Fundamental rule no. 1! If we can pair ℕ and ℤ, we are good to go. How about this pairing?

This works perfectly because no integer will be left out, and each one will have a pair in ℕ, which is its index in the sequence. So, to translate this, two times countably infinite is still countably infinite.

An important note. Pairing something with ℕ is the same as writing them in a sequence such that no element is left out, because the first element will be paired with 1, the second with 2, and so on.

Thus, the sequence 0, 1, -1, 2, -2, … defines the pairing above. This is called an enumeration.

Let’s see another example!

Example 2. The set of odd numbers: {1, 3, 5, 7, …}

Using the previous trick, it is obvious that there are as many odd numbers as natural numbers. Half of countably infinite is still countably infinite!

Example 3. The set of prime numbers: {2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, ...}

I am not going to go into details, but let that sink in: there are as many prime numbers as natural numbers, even though they are extremely rare once we start to go beyond! There are arbitrarily large gaps between two consecutive prime numbers, so this is kind of awesome.

Let’s see one more example!

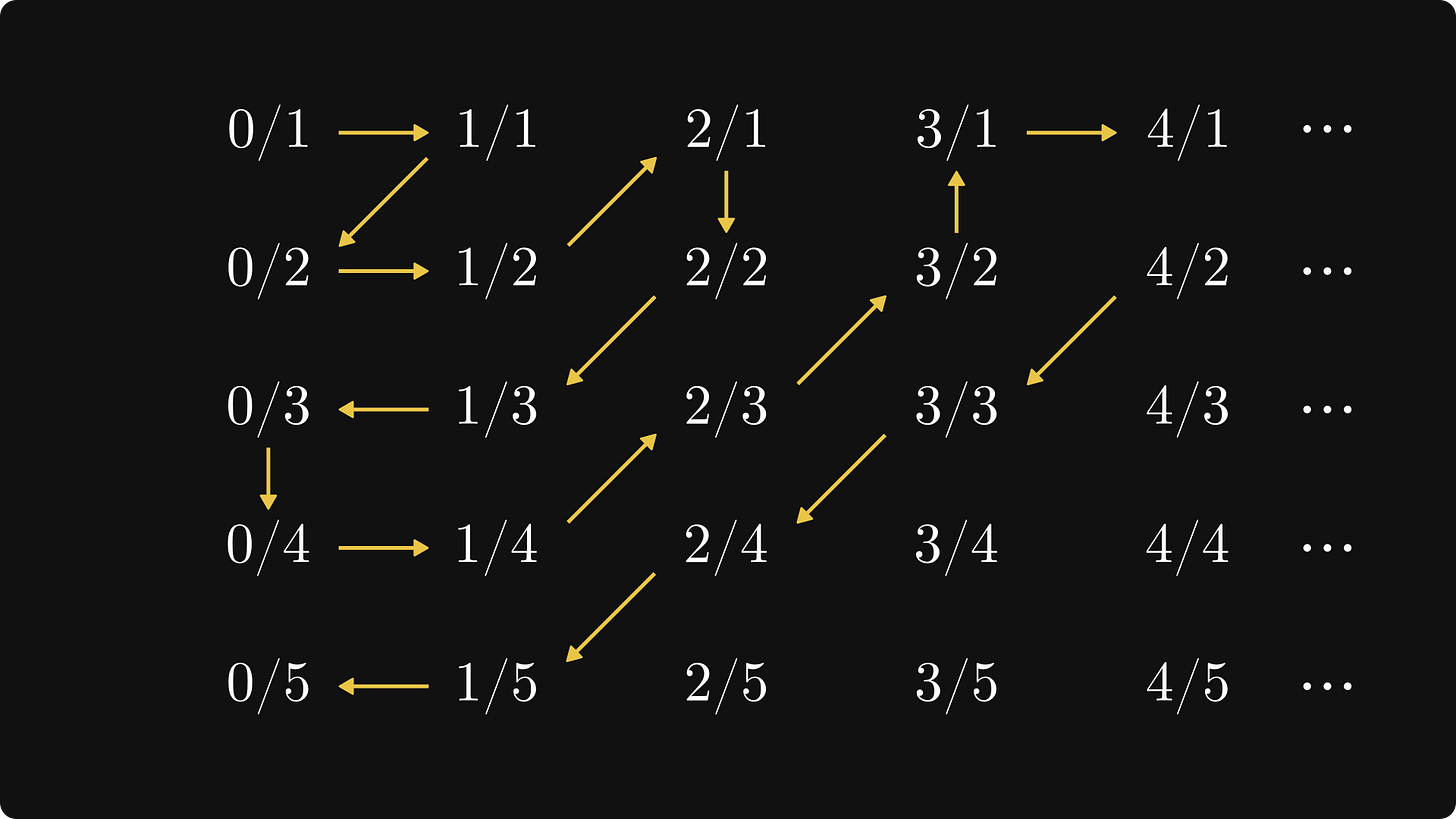
Example 4. The set of rational numbers (ℚ). A number is rational if it can be written as the ratio of two integers, that is, p/q for some integers p and q. Let’s write down all rational numbers! (Forget about the negative ones for simplicity, every argument goes through identically in the general case.)

Listing the rational numbers

So, there is a countably infinite number of rows containing countably infinite numbers. See why infinity is mind-boggling? Countably infinite times countably infinite is countably infinite. How can we see this? Just enumerate them using a clever ordering:

Enumerating the rational numbers

To test whether you understand these concepts, you should come up with an argument for

• why is the statement also true if we include negative rational numbers,

• and why it’s not a problem that 0 is enumerated multiple times.

Beyond countable

So, are there sets that are larger than countable? Yes!

The first example is the set of real numbers (ℝ). They are defined as the union of rational and irrational numbers. Irrational numbers are those real numbers that cannot be expressed as a ratio of two integers, like π, e, and the square root of 2.

(There is a bit of circular argument here, as we cannot define reals as the union of rationals and irrationals if we define irrationals as the non-rational reals. Behind the scenes, there is some advanced stuff going on, see the Cauchy completion of metric spaces. Kudos to you if you caught the logical fallacy before I pointed it out :) )

How do we know that the real numbers are larger than countably infinite? First, we know that they are at least countable, because they contain the natural numbers as a subset. (See Fundamental rule no. 2.) So, let’s try to enumerate them!

For simplicity, focus only on numbers between 0 and 1, that is, in the interval [0, 1). Suppose we did enumerate those numbers successfully. Each of them can be written down in decimal like 0.a₁a₂a₃... where a₁, a₂, … are the digits of the first one.

Something like this:

Since we have enumerated them, we are free to write them on top of each other.

Now, prepare to be mindblown. Let’s take a look at the digits along the diagonal, that is, those digits which I highlighted with yellow: