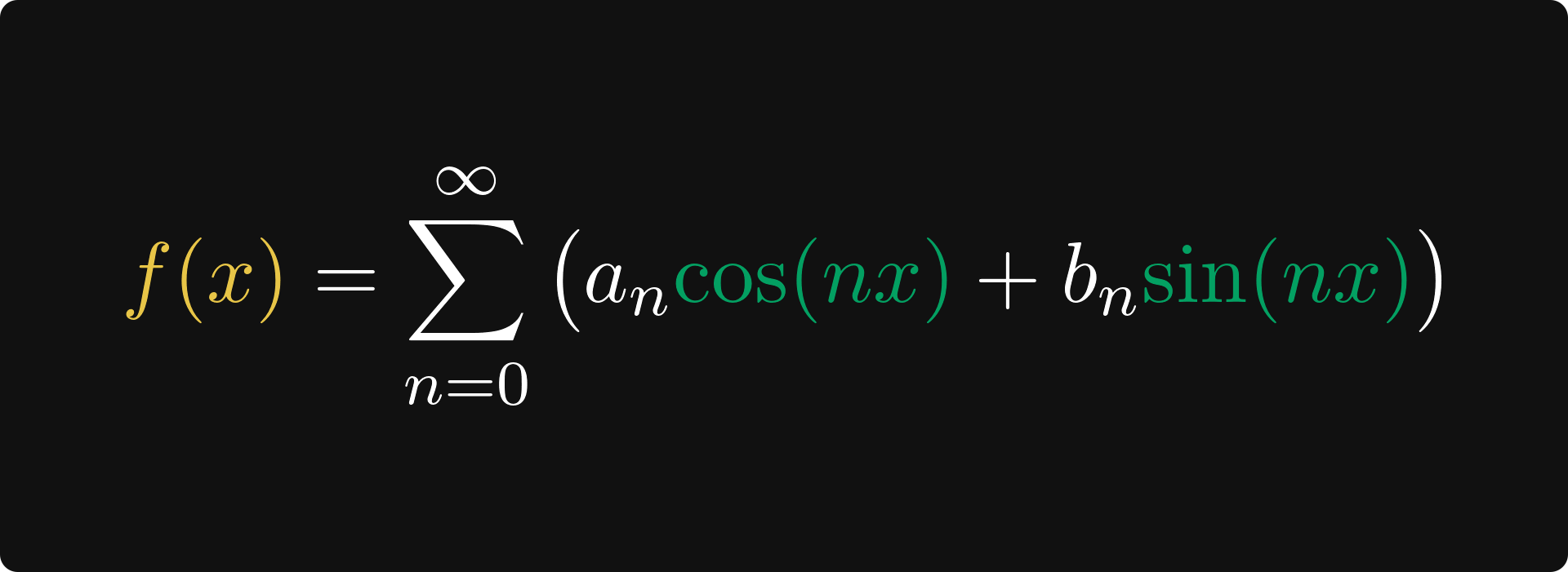The unreasonable effectiveness of orthogonal systems
Decomposing complex objects into a sum of simple parts
Last week, we have talked about the all-important concept of orthogonality. At least, on the surface. Deep down, the previous post was about an extremely important idea: finding the right viewpoint is half the success in mathematics.
We illustrated this through the concept of vector spaces, inner products, and orthogonality. Through clever representations, we can stretch mathematical definitions to objects that seemingly lie far from the original domain. Functions as vectors? Check. Riemann integral as an inner product? Check. Enclosed angle by functions? Once more, check.
This time, we’ll continue on this thread. Today, the core idea in the spotlight: decomposing complex objects into simple parts. Believe it or not, this is behind the stunning success of modern science.
(If the title of the post is familiar, it is not an accident. It is a reference to the classical paper “The Unreasonable Effectiveness of Mathematics in the Natural Sciences“ by Eugene Wigner.)