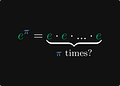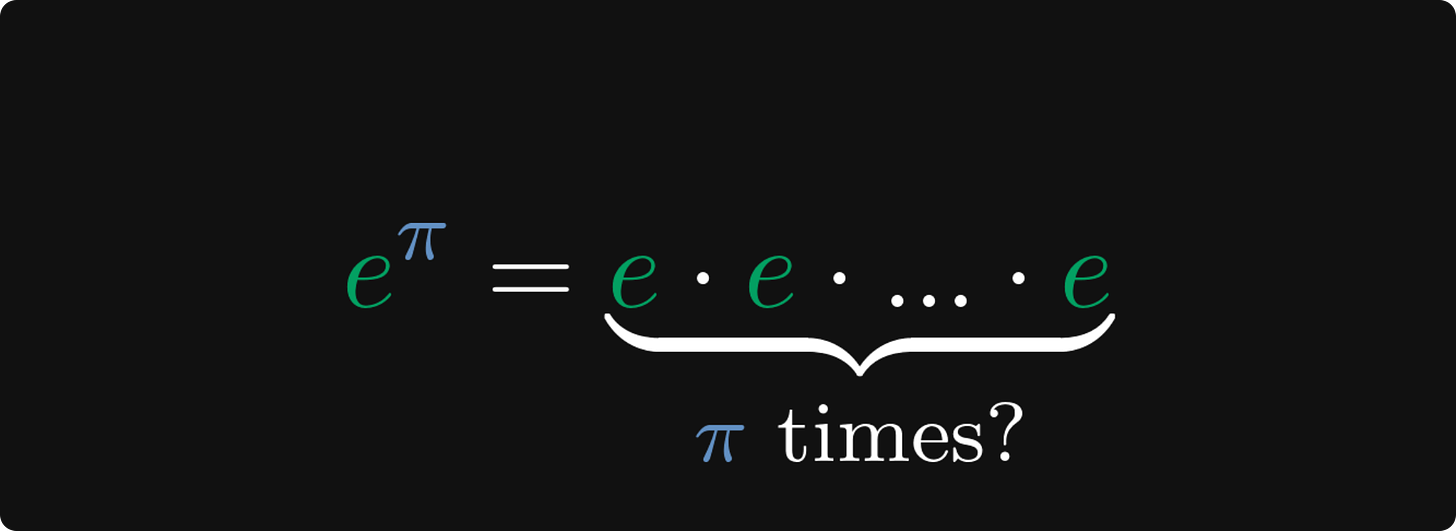The way you think about the exponential function is (probably) wrong.
Don't think so? I'll convince you. Did you realize that multiplying e by itself π times doesn't make sense?
Here is what's really behind the most important function of all time.
The exponential
First things first: terminologies. The expression aᵇ is read "a raised to the power of b." (Or a to the b in short.)
Keep reading with a 7-day free trial
Subscribe to The Palindrome to keep reading this post and get 7 days of free access to the full post archives.