The Camel Principle
What it is, how it works, and why it is essential
Behold one of the mightiest tools in mathematics: the camel principle.
I am dead serious. Deep down, this tiny rule is the cog in many methods. Ones that you use every day. Here is what it is, how it works, and why it is essential.
First, the story. The old Arab passes away, leaving half of his fortune to his eldest son, third to his middle son, and ninth to his smallest. Upon opening the stable, they realize the old man had 17 camels.
This is a problem, as they cannot split 17 camels into 1/2, 1/3, and 1/9 without cutting some into parts.
So, they turn to the wise neighbor for advice. The wise man says, “Hold my camel,” and solves the problem by lending one to the boys.
Now the stable has 18. The eldest son takes 9 home, while the middle and smallest son leaves with 6 and 2, as their father wished.
The wise man takes his camel back, and everybody is happy.
Thus, the camel principle is born: adding and subtracting the same quantity doesn’t change the equality, but can help in the computation.
In mathematics, you cannot live without this principle. I'll show you two examples.
The first one is the quadratic equation. Its solution formula is one of the few things everyone remembers from high school, even if they are woken up in the middle of the night.
This formula is derived from the camel principle. Let me show you how!
After factoring out 𝑎 from the equation, we notice that the famous identity (α + β)² = α² + 2αβ + β² might help to factor the quadratic equation into a product. To achieve that, we apply the camel principle!
After adding and subtracting the same quantity, the terms with 𝑥 factor into a product.
Since the product of two terms is zero if either term is zero, this move leads straight to the solution formula.
There is an alternative version of the camel principle, performing a similar feat: multiplying and dividing with the same quantity. This doesn’t change the equality either.
To illustrate, let’s look at derivatives, the main engine behind mathematics, physics, and optimization. (And tons of other fields that allowed technology to get where it is now.)
Here’s the definition, taking the limit of the difference quotient as x gets closer to a.
How would you calculate the derivative of a composite function?
This is a quintessential question. Without this, you don’t have backpropagation, gradient descent, and thus neural networks. (At least until someone invents a clever alternative. But that’ll take a while.)
Here’s the limit that we have to compute.
You guessed right: the camel principle! (At least, the second version, where you multiply and divide with the same quantity.)
Check it out. First, we insert the term g(x) - g(a) between the numerator and the denominator.
With this, both the derivatives of f and g make an appearance.
After the camel principle is applied, we carry out the limit termwise. (For those with the eagle’s eyes: yes, the denominator can be zero. You can epsilon-delta your way out of that, but I won’t do it here.)
And thus, we have the chain rule, one massive pillar of science and technology.
This is what we use to perform backpropagation, enabling us to train our neural networks in a reasonable time.
The lesson here: tiny mathematical curios such as the camel principle are often dismissed as “lacking any applications”. However, such short-sightedness can lead us astray.
By understanding atoms, you are able to build skyscrapers.








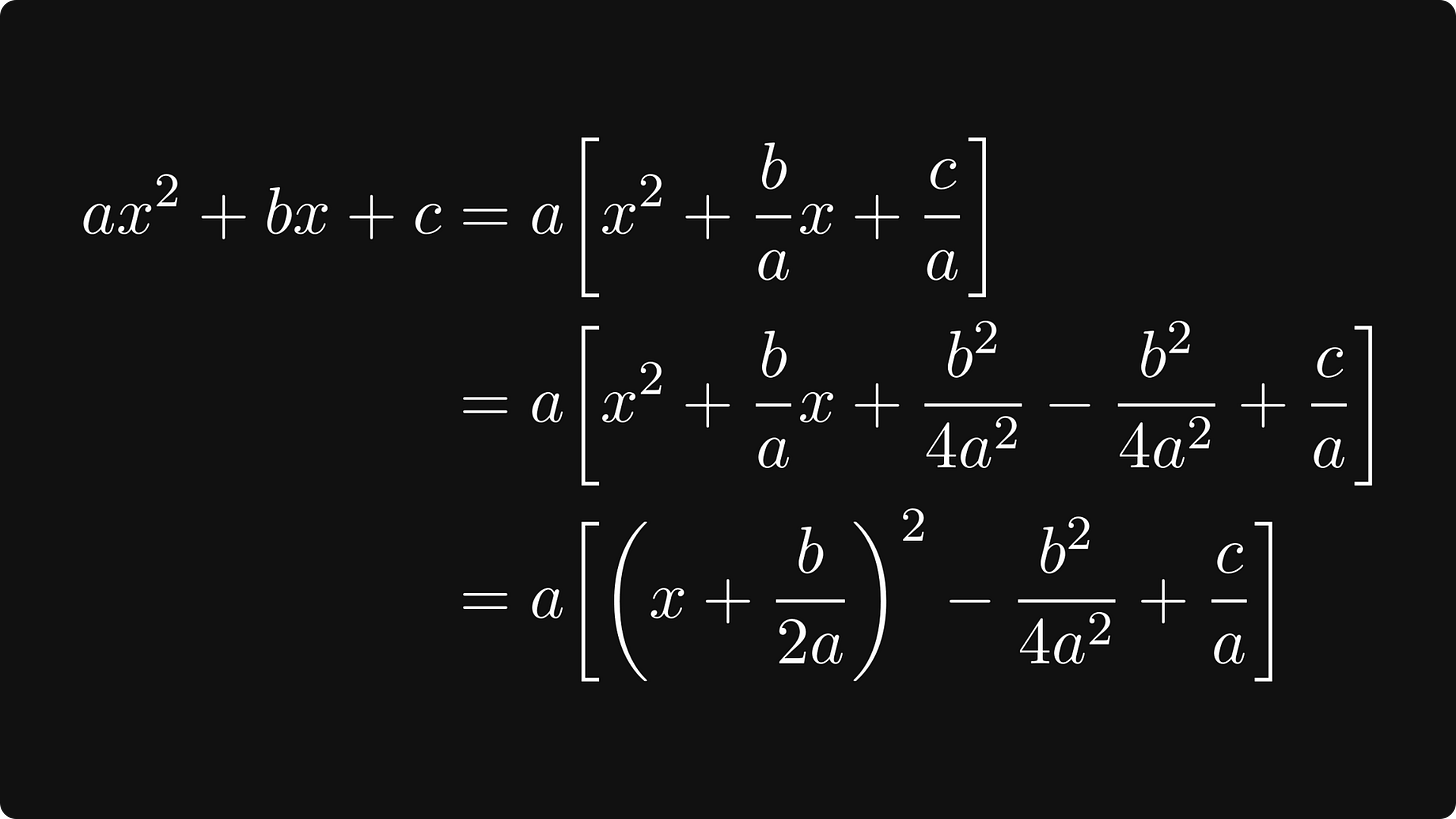
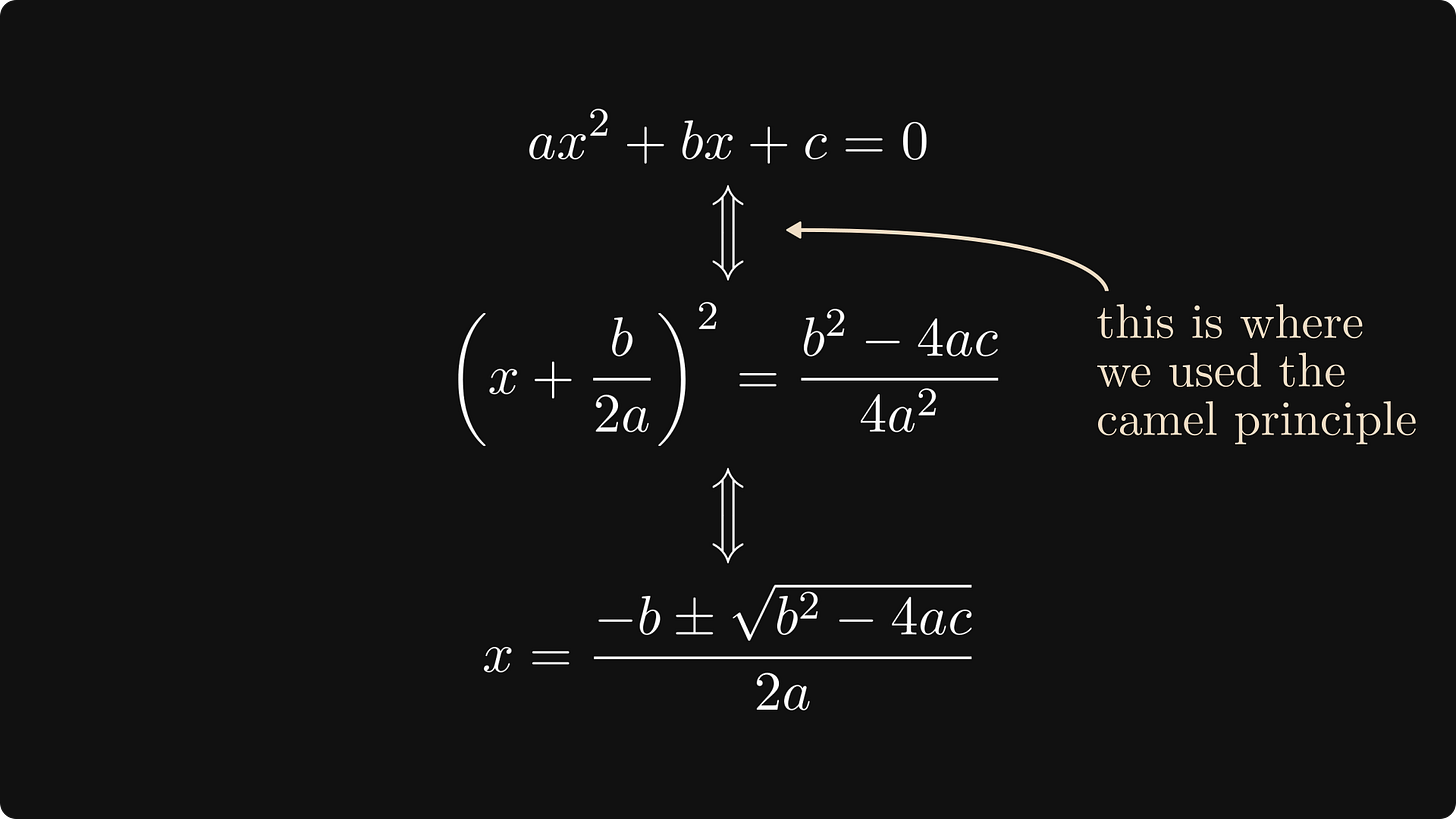





The beauty of math is not to use as many words as possible but as little as possible. You are literally taking something that is supposed to create clarity and use it remove clarity. What you mean is simply:
1/2 + 1/3 + 1/9 = 0.9444 != 1
So if the arab was going to leave 1/2 to the first son, 1/3 to the second son, and 1/9 to the third son, what was he planning on doing with the remaining 1/18?
Not everybody can be happy, because that 1/18 of a camel should go to someone, but nobody received it!