How to Measure Information
A deep dive into entropy
Hi there! It’s Tivadar from The Palindrome.
Today’s post is a guest post by Ameer Saleem, the author of theMachine Learning Algorithms Unpacked Substack.
I first encountered Ameer’s work a couple of months ago, and I was blown away by the quality and precision of his explanations. Just like me, he is a fan of taking algorithms apart and building them from scratch, understanding the role of every nut and bolt in the process.
We got in touch, started working together, and this is the first post in what we hope will be a long line of collaborations. If you have enjoyed this, make sure to subscribe to Machine Learning Algorithms Unpacked!
Cheers,
Tivadar
Hello fellow machine learners,
Today, we will discuss the topic of information entropy. I remember learning about this concept at university. More specifically, I remember the drum roll moment where the formula for information entropy was displayed during the lecture:
And my brain went:
“Ah, I see, yeah, that makes perfect sense…
… actually, I don’t know what the heck I’m looking at.”
The explanations we were given in lectures felt quite confusing to me, in part because we were trying to ascribe mathematical formulas to rather abstract concepts like information and uncertainty.
For example, what has the logarithm got to do with the flow of information? And why base 2?
This post is about the intuition and the science behind information and entropy, two of the most important quantities of data science and machine learning.
These concepts were first mathematically formalised by Claude Elwood Shannon in his revolutionary 1948 paper titled “A Mathematical Theory of Communication”. This is the main reason why Shannon is regarded as the founding father of information theory. As well as this, Anthropic’s Claude AI model was named after Shannon. So, he’s a pretty big deal.
With all that said, let’s get stuck in!
📌 The Palindrome breaks down advanced math and machine learning concepts with visuals that make everything click.
Join the premium tier to get access to the upcoming live courses on Neural Networks from Scratch and Mathematics of Machine Learning.
How do we measure information?
What is your standard breakfast? It might be a bowl of cereal. Suppose that you make yourself a bowl of, say, cornflakes in the morning. You take a spoon and eat a mouthful.
It tastes like… cornflakes. Well yes, of course it does. No surprises there, right?
But what if the milk you used was actually expired, and you didn’t realise beforehand? Then you’ll instead be greeted with a repugnant taste. In this case, you’d be pretty surprised – and perhaps a tad nauseous.
In the case of the second event, the action of eating your cereal has provided new information. (In particular, you now know that you need to get some new milk!)
Let's consider another example; a more mathematical one to help formalize our intuition.
Suppose you have a die that you know is heavily biased toward landing on the number 6. If you rolled the die and had to predict what number it would land on, what would you predict? Well, 6 of course. And in doing so, you’d probably be right most of the time. You already know the bias of the die, and so you won’t be surprised from seeing the outcomes of its rolls.
What if, instead, the die is fair, i.e. each number is equally likely to be rolled? Well, you could guess any number and, chances are, you would be wrong more times that you’d be right. After all, for each roll of the die you would only have a one-in-six chance of guessing the number correctly. That is, most of the time, you will be surprised when seeing the outcome of its rolls.
Thus, we can consider the roll of the second die to provide us with more information than the roll of the first die.
Intuitively, we could think of information as follows:
“The amount of information an event provides can be quantified by how surprising the event’s occurrences are. The more surprising an outcome, the more information you gain from seeing the outcome.”
How can we turn our intuition into a mathematical definition?
Suppose that an event occurs with probability p. If we wanted to mathematically define the information gained from observing the outcome that occurs with probability p, how would we do it?
You can think of information as a function I(p) that maps a probability to, well, it's information content. Whatever function we plan on using, we want the following conditions to hold:
The function I(p) should be continuous. The value of information gained (or lost) should change smoothly as the value of p changes.
If p=1, then our information function should output the value 0. This is because, if an event that occurs 100% of the time, then we do not gain any information at all from observing its outcome, i.e. no surprise.
The total information gained from two independent events should equal the sum of the information gained from each individual event.
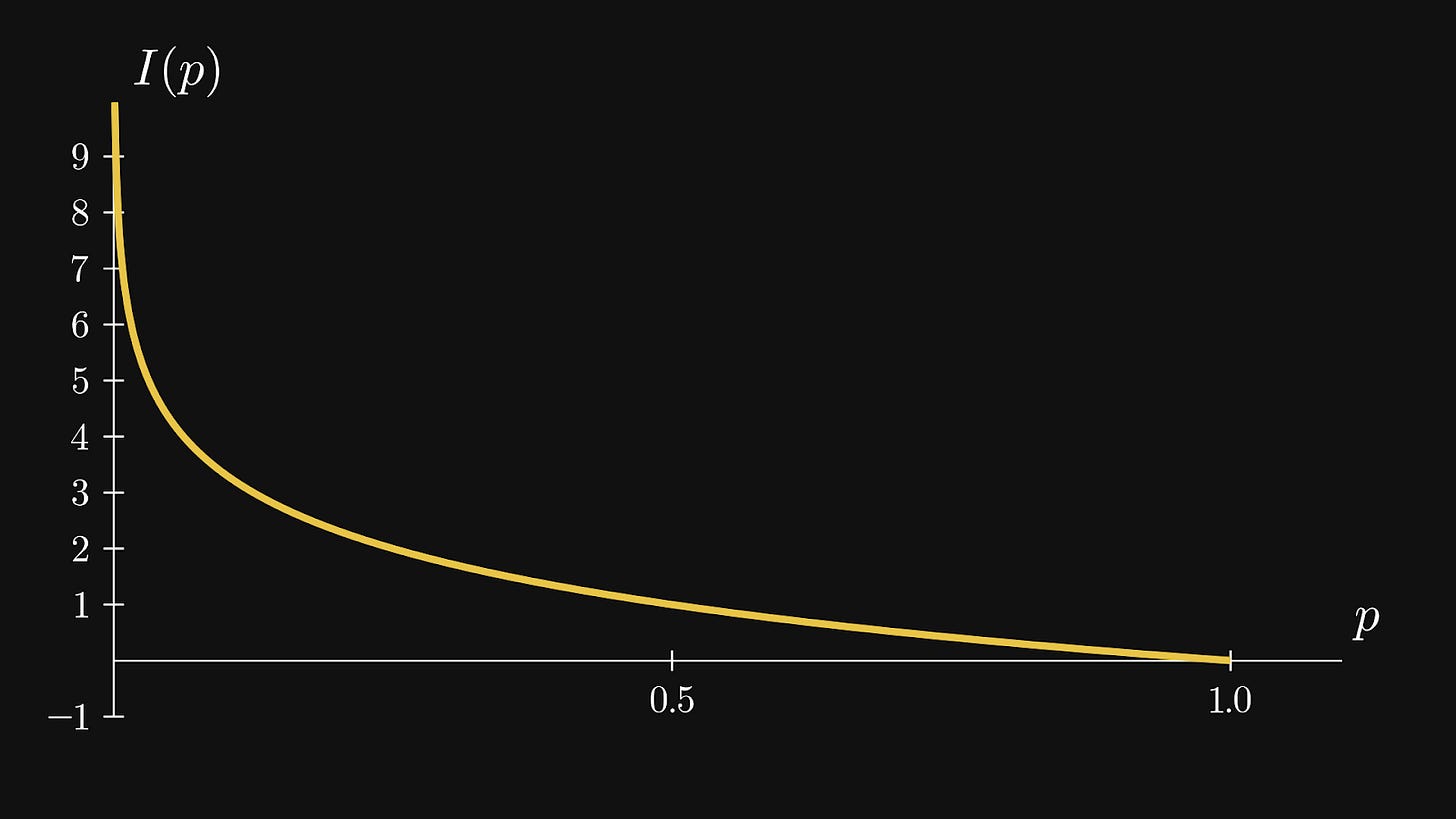
The more unlikely an event is, the more surprise there is when sampling its outcomes. So the function should be large when p is small, and small when p is large.
These criteria are satisfied precisely by the so-called self-information function
We will explain the use of the base-2 logarithm specifically later. For now, we can check that this function satisfies our requirements:
Continuity: the logarithm is a continuous function.
Zero information for a deterministic outcome: when p=1, the logarithm takes the value 0 as desired.
Joint events: suppose that we have two independent events which have probabilities p₁ and p₂ of occurring respectively. Then we have by the additive property of the logarithm that
(Recall that two events A and B are independent if
that is, if the probability of both A and B occurring is the product of the two probabilities.)
Here is what the function looks like, demonstrating that condition 4 is indeed satisfied:
Information entropy
Claude Shannon formalised the idea of information entropy mathematically. Given a set of possible events whose probabilities of occurrence are given by the distribution P = (p₁, p₂, …, pₙ), the information entropy of the set of events is given by the expected value of the self-information provided by a probability distribution. The formula is given by
Suppose that the random variable X follows a Bernoulli distribution of parameter p. That is, it takes the value 1 with probability p, and takes the value 0 with probability 1 - p:
The entropy of this corresponding distribution is
The following animation shows the value of the entropy function for different values of p:
So the information entropy is maximised when p = 0.5 which corresponds to the fair coin toss example. In this case, the information entropy value is
Conversely, the minimum value that entropy can take is 0. In the Bernoulli distribution case, this happens when either p = 1 or p = 0.
At this stage, we’ve discussed the intuition behind the use of the logarithm. But if you have another look at the formula for Shannon entropy, you may realise that there is one more question that has yet to be answered…
Why we use base 2 in the logarithm?
Suppose that I am in a room with a coin and a light switch, and my friend in a separate room wants to know whether the coin lands on heads or tails when I toss it, and he wants to know without leaving his room. I am not allowed to communicate with him in any way except with the audible sound of the light switch flip. However, we are allowed to discuss a strategy before we each go into our separate rooms.
The question is as follows: what is the most efficient way I can communicate to my friend whether the coin landed on heads or tails?
One way to do this is with Morse code. I could flip the coin and then the light switch to communicate either ‘head’ or ‘tail’ in Morse code. This would certainly inform my friend of the coin’s toss outcome…
…but can we be even more efficient?
We could agree the following before breaking off: if the coin lands on heads, I flip the switch just once; otherwise, I don’t flip the switch at all. Then my friend can enter his room and just wait for, say, 60 seconds before knowing what has happened.
In deciding to flip the light switch just once, I have transmitted one bit of information to my friend. A bit of data is the smallest measurable unit of information. A bit can take one of two values: 1 or 0. These numbers correspond to either flipping the light switch or leaving it be.
This is far more efficient than using Morse code for the letters of the alphabet. In fact, this one-bit approach is the most information-efficient way in which we could’ve communicated the outcome of the coin toss. And we are saying that I need at least one bit of information to communicate the coin toss outcome to my friend.
Simple communication tasks can be encoded using binary. The binary system is a number system that uses only 0s and 1s, rather than the 0-9 digit decimal system that we use more commonly. Each new column in the binary system introduces the next highest power of 2. So our regular numbers like 3, 12, 1028496839, etc. all have binary representations.
So to work out how many bits are needed to store a value, we need to know what power of 2 we’ll need. And this information is provided precisely by the base-2 logarithm. Don’t forget that logₐ(b) means “what power do I need to raise the value a to in order to get the value b?”.
Thus, the base-2 logarithm is used in the self-information and information entropy formulas, because it tells us how many bits are needed to store the desired information, and bits are the standard unit measurement to store information. Different bases will tell you how many units are needed in a separate digit system. For example, the natural logarithm, which uses the number e as its base, uses the units of ‘nats’ (which I assume stands for ‘natural bits’?).
Packing it all up
We’ve learned that the ‘surprise’ from seeing the outcome of an event can be quantified with the self-information function. This function obeys some intuitive rules around continuity and independent events. And the feature of this article, the information entropy, is nothing more than the expected value of the self-information function for a given probability distribution! Entropy is maximised for discrete distributions where all the outcomes are equally likely. Conversely, the more skewed a distribution, the lower the entropy because, intuitively, there is less surprise in seeing the outcome.
The information gained from seeing the outcome of an event can be quantified by measuring how surprising the event’s outcome is. This is quantified by the self-information function, defined by the base 2 logarithm of the probability.
On top of the self-information function, entropy is given by the expected value of information provided by the outcomes of a probability distribution.
Entropy is maximised for discrete uniform distributions, and is minimised when the outcome of an event is guaranteed. The more skewed a distribution is, the less surprising its outcomes will be.
The base-2 logarithm tells us how many bits are needed to store the desired input information. Different bases measure the information storage size in the corresponding number system. Pretty cool, huh?
Training complete!
I hope you enjoyed reading as much as I enjoyed writing 😁
Do leave a comment if you’re unsure about anything, if you think I’ve made a mistake somewhere, or if you have a suggestion for what we should learn about next 😎
Ameer



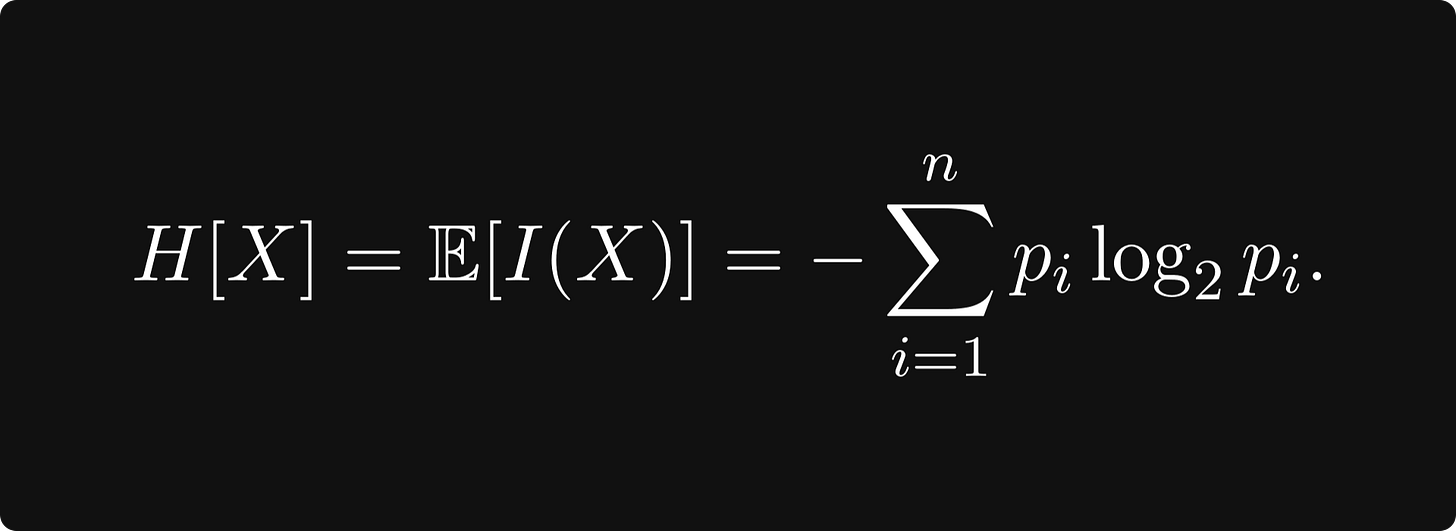
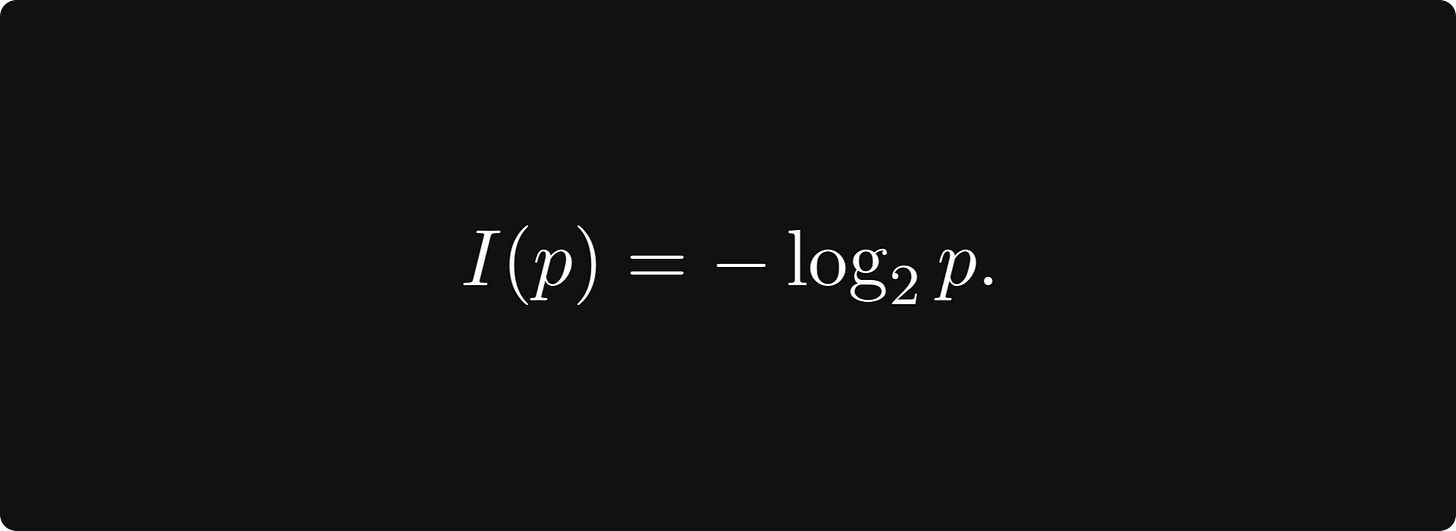
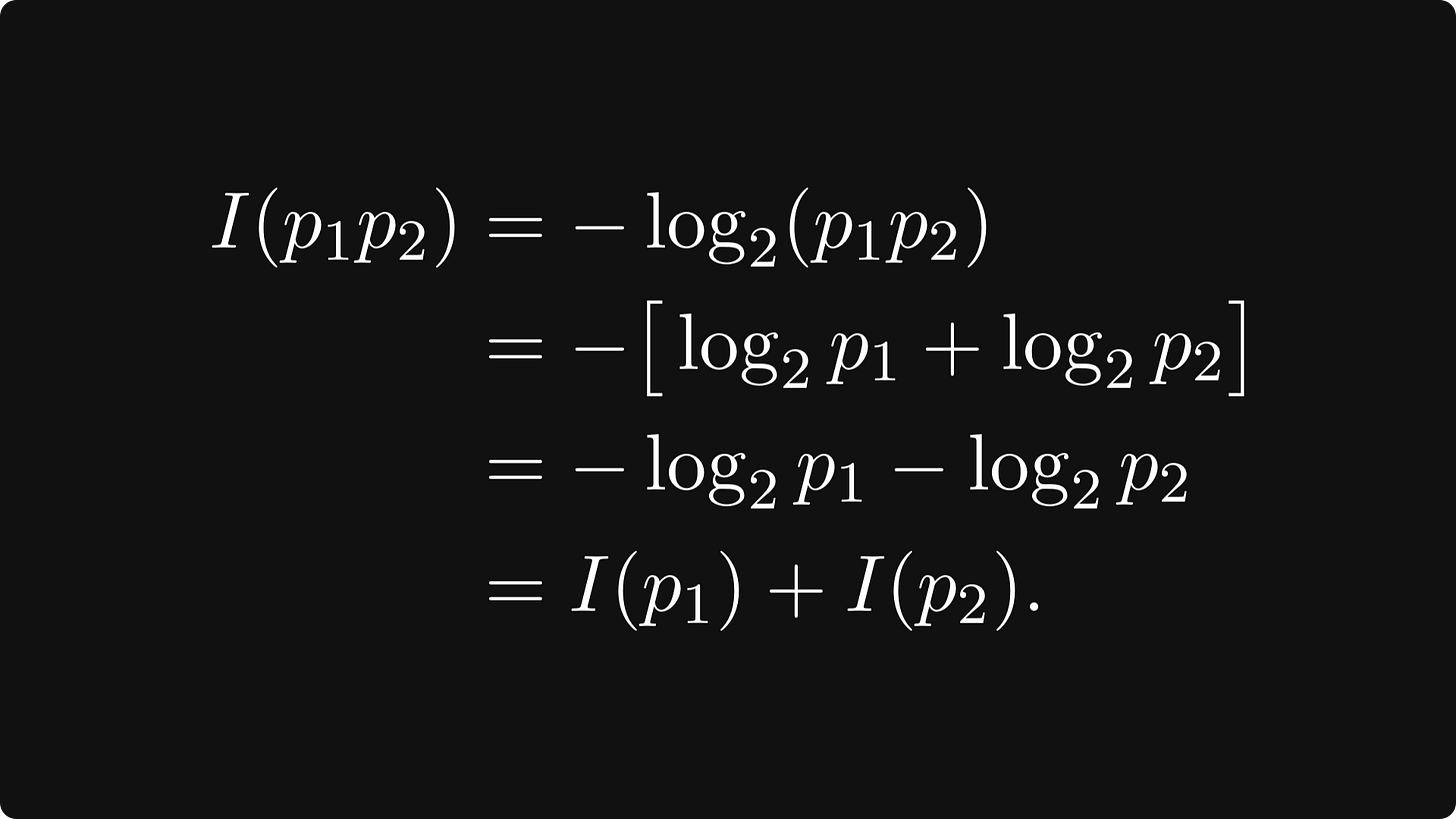
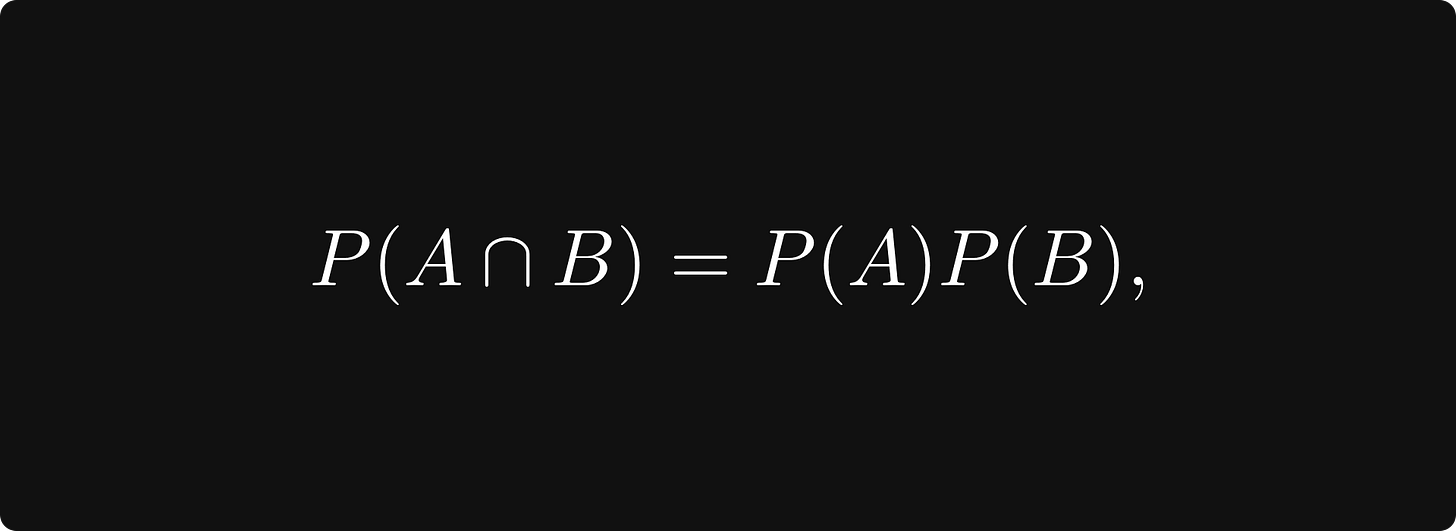
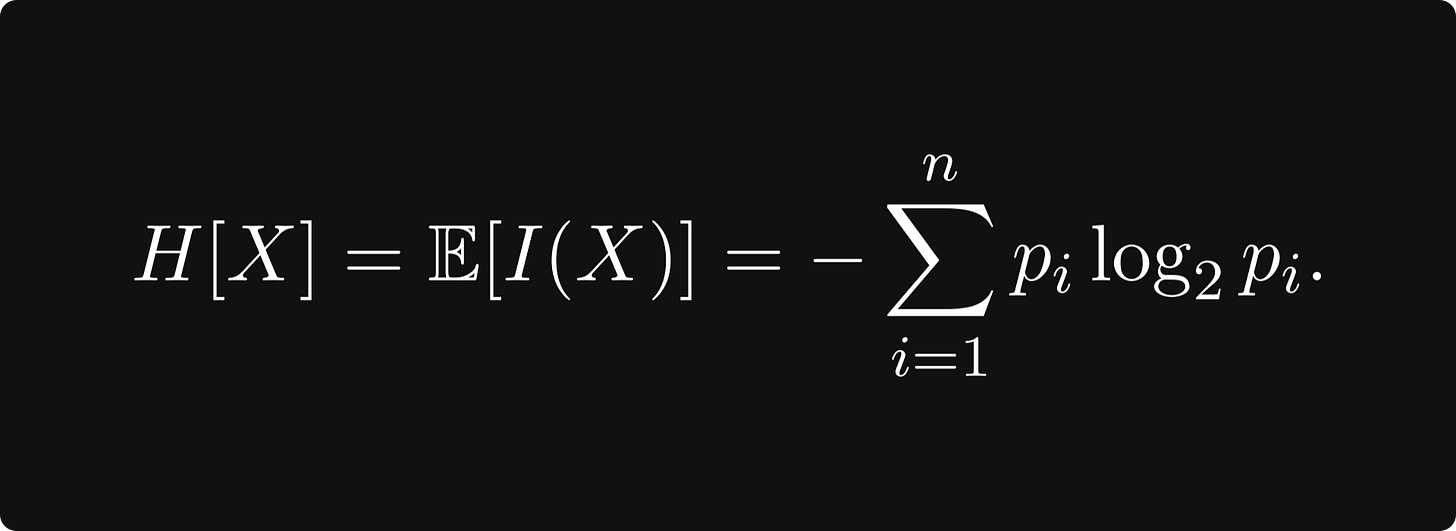
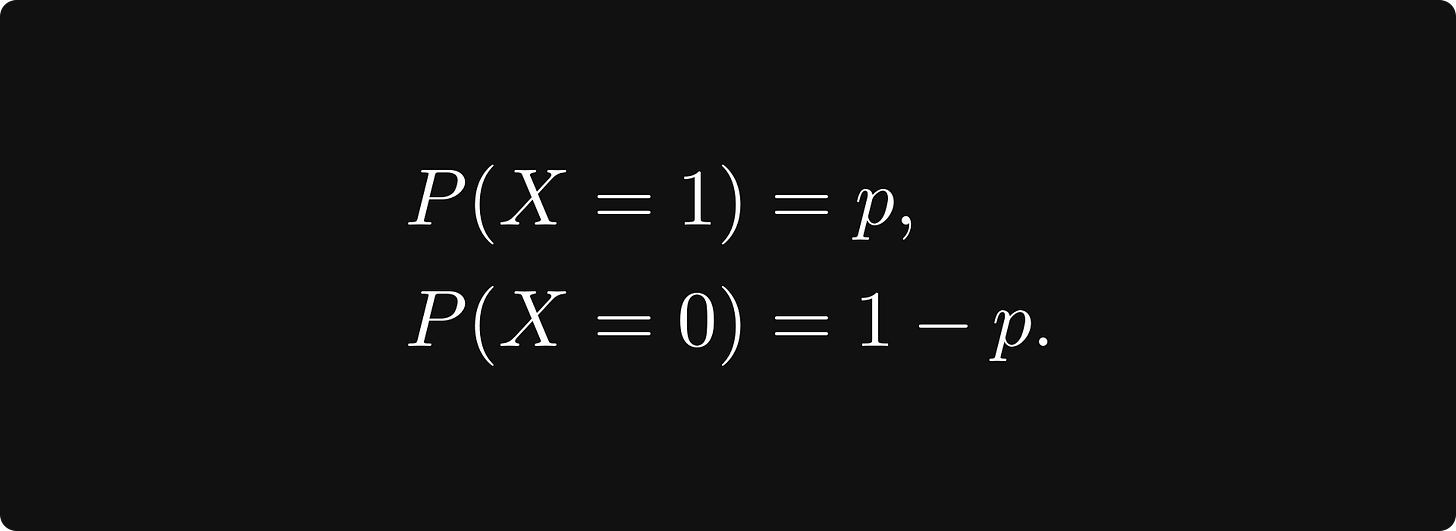
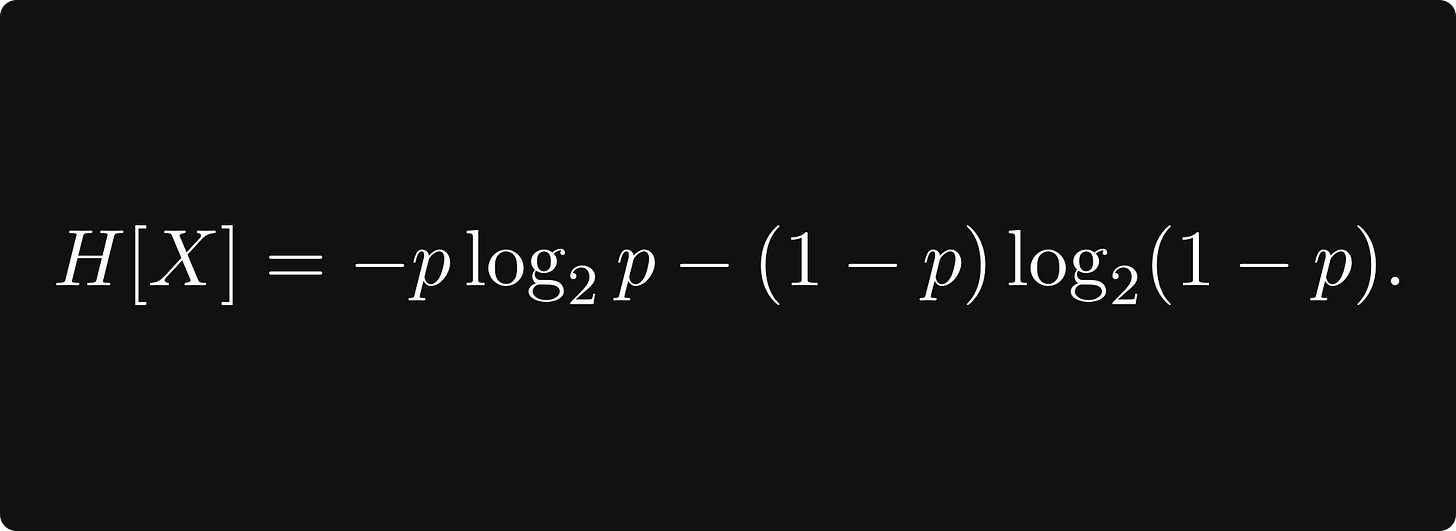
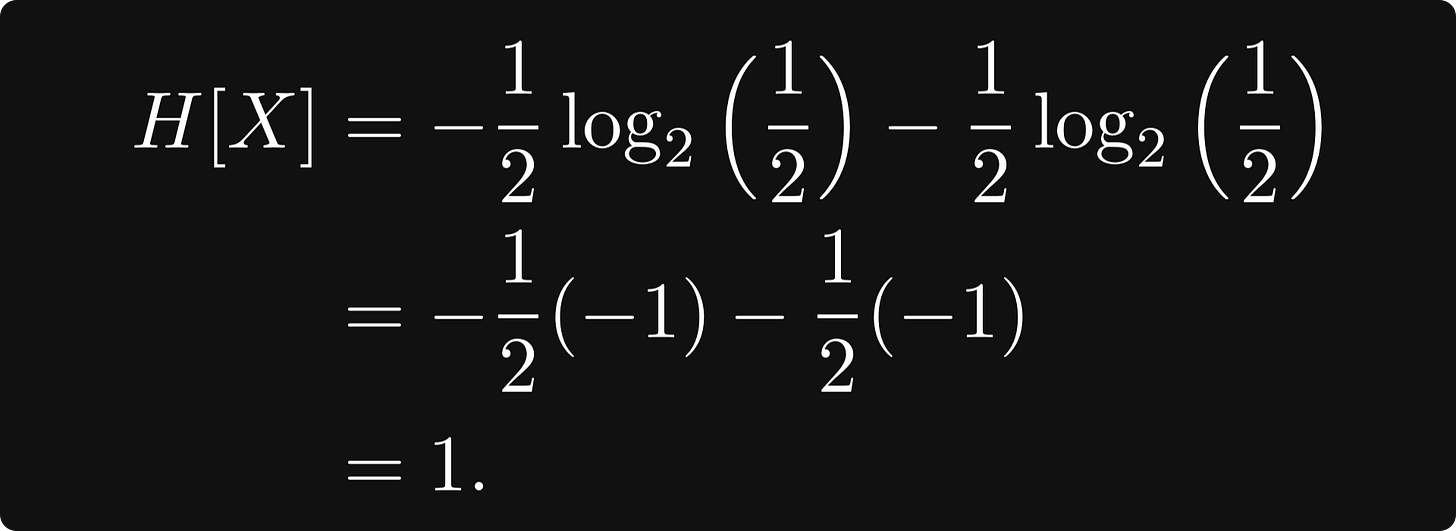

Was great to collaborate on this with you Tivadar 😁 hope you all enjoy
Awesome post. The quality of guest authors in this newsletter is top notch.