Min-Max Math, ep. 05: Proofs are (not) magic
Any sufficiently advanced mathematical trick is indistinguishable from magic
I am a 90’s kid. One of the biggest pop-cultural moments of my childhood was David Copperfield making the Statue of Liberty disappear.
I know: the original performance took place in 1983, but I was born on the eastern side of the Iron Curtain, and we had no commercial TV channels up until around 1996. So, with a whopping 15 years of delay, I got to see the great show, and it felt unreal. It felt magic.
However, magic does not exist. We know exactly how the feat was done.
Now, why is mathematics considered difficult? There is a plethora of reasons, but the biggest jump you have to make is from intuition to proof. Reading and writing proofs are hard, but you cannot get away without them.
The power of mathematics comes from proofs. And abstraction. And thinking patterns. And…
Let’s focus on proofs for now.
Proofs feel like magic. However, magic does not exist, and we’ll look behind the curtain now.
To make the concept of proof truly ours, we’ll study a classical example, one that you are already familiar with: the famous Pythagorean theorem.
This post is a free episode from my Min-Max Math course, exclusive for paid subscribers. Instead of convoluted results and technical details, we’ll have weekly lessons about
the tools of (mathematical) thinking,
the fundamental mathematical objects,
and how they relate to life, science, and technology.
Sign up for full access!
The Pythagorean theorem
There is a famous law in called Stigler's law of eponymy, stating that no scientific discovery is named after its original discoverer.
Stigler’s law was discovered by American sociologist Robert K. Merton. Besides itself, it also applies to arguably the most famous mathematical result, the Pythagorean theorem. This geometric proposition was known even to the ancient Egyptians!
It's a fundamental part of our culture and knowledge.
Here it is in its full glory.
Theorem. (The Pythagorean theorem.) Let ABC be a right triangle, let a and b be the length of its two legs, and let c be the length of its hypotenuse.
Then a² + b² = c².
Let’s shoot first and ask questions later: here is the proof in its full glory.
Proof. Mathematical proofs often feel like pulling a rabbit out of a hat. I’ll go a bit overboard and start by pulling out two rabbits.
The first rabbit. Take a look at the following picture.
The depicted square’s side is a + b long, and hence, its area is (a + b)². Our square can be dissected into six parts:
a square of side a and area a²,
a square of side b and area b²,
and four congruent right triangles of sides a, b, c, and area ab/2.
By summing up the areas, we conclude that (a + b)² = a² + b² + 2ab.
Now, the second rabbit. Again, take a look at the following picture.
Once more, the depicted square’s side is a + b long, and its area is (a + b)². However, this time, it is partitioned into five geometric shapes:
a square of side c and area c²,
and four congruent right triangles of sides a, b, c, and area ab/2.
Like before, we conclude that (a + b)² = c² + 2ab.
However, as both of the enveloping squares have an area of (a + b)², we get that a² + b² + 2ab = c² + 2ab, which implies a² + b² = c².
This is what we had to show. ◼
Now, it’s time to peek behind the curtain. To lift the veil. To dissolve the notion that mathematical proofs are magic.
To turn magic into a method.
From magic to method
If you pay attention to the above proof of Pythagoras’ theorem, you can notice that the proof itself consists of two parts. First, there is an idea; a spark that ignites the fuse. A spring from which the river flows.
Second, there is a logical argument. That river which flows from the spring that is our idea.
The idea is simple: we cut up the same square in two different ways, and conclude that the corresponding areas must match.
Where do we conjure that idea from?
There are several go-to problem-solving strategies, but as we are dealing with a geometric problem, let’s think visually.
As a², b², and c² imply that there are squares in the play here, this is the first image that comes to mind.
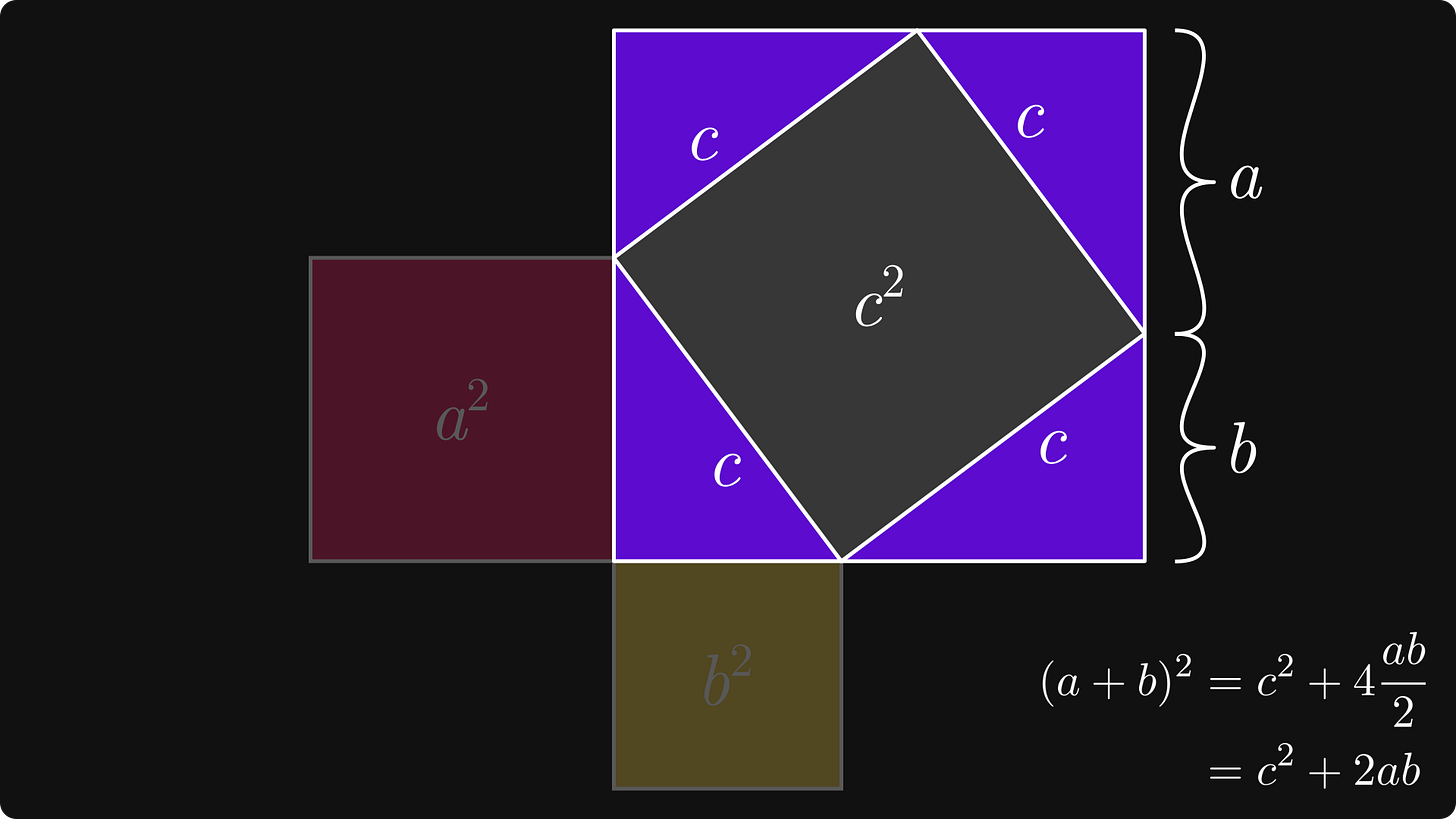
These squares come from the same source: our right triangle. We can connect them together using this.
Our goal is to show that the red and yellow squares add up to the gray one.
What can we do with this figure?
Using our internal pattern matching system (a.k.a. our brain), we can extend this figure in two different ways. First, we can fill the blanks at the bottom left corner with triangles that are congruent to our original right triangle.
This yields (a + b)² = a² + b² + 2ab.
Second, is by doing the same fill-the-blanks game around the sides of c².
Again, this yields (a + b)² = c² + 2ab.
Thanks to our observations, we now have two identities:
(a + b)² = a² + b² + 2ab, and
(a + b)² = c² + 2ab.
This was the idea part.
From this point, the execution phase is simple. We’ll rely on two fundamental truths, that is, axioms¹:
If x equals to y and y equals to z, then x equals to z as well.
(That is, [x = y] ∧ [y = z] → [x = z].)If x equals to y and z equals to w, then x + z equals to y + w as well.
(That is, [x = y] ∧ [z = w] → [x + z = y + w].)
We can apply these via modus ponens. Breaking it down to every last step, this is what happens:
Thus, with a clever idea and a chain of implications, we’ve proved the Pythagorean theorem.
There are two burning questions remain. Where do we get our ideas from? How do we know what to prove? I wish there would be an answer. I wish I knew the answer. But there are no algorithms, no sure methods. "There is no royal road to geometry", Euclid famously claimed. It’s not just for geometry: it applies to everything.
This is the (he)art of mathematics.
"If only I had the theorems! Then I should find the proofs easily enough." — Bernhard Riemann
Summary
Why is mathematics difficult? Over my 15+ years as a mathematician, I have asked this question hundreds of times. Both from myself and from others.
One of the most commonly cited reason is reading and writing proofs.
Proofs seem like magic: mathematicians conjure ideas and tricks just like magicians pull rabbits from hats. This is the hard part. Good news: use it once, and it’s a trick; use it twice, and it’s a method.
There are methods to the madness. And we’ll pick them up one by one.
Footnotes
¹ In the precise axiomatic formulation of mathematics, these propositions are not axioms, but theorems. However, in Euclid’s elements, these were indeed axioms.
You can find the previous episodes of the Min-Max Math series here.











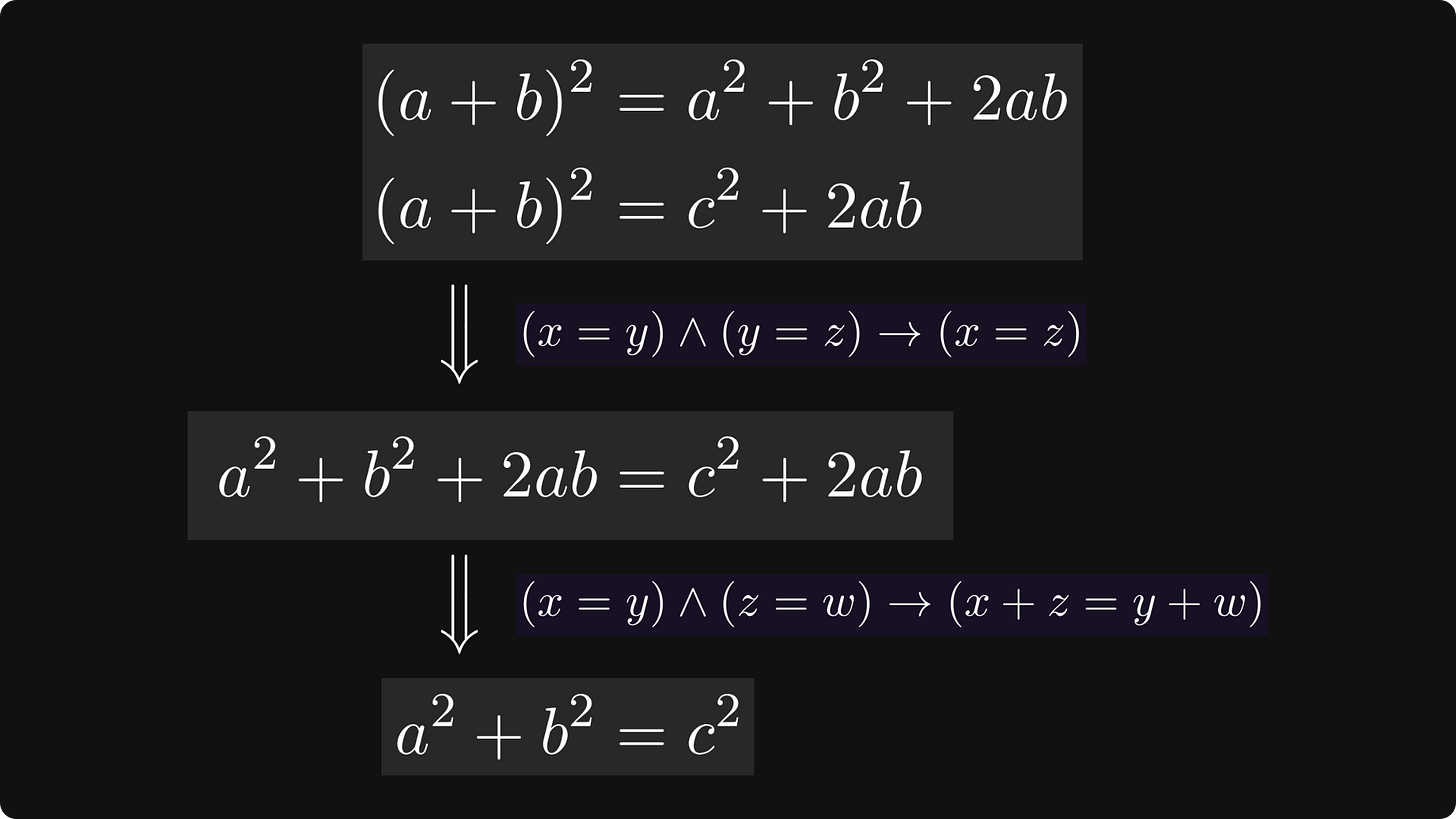
absolutely brilliant !
The way you explained it is amazing! Appreciate your work.