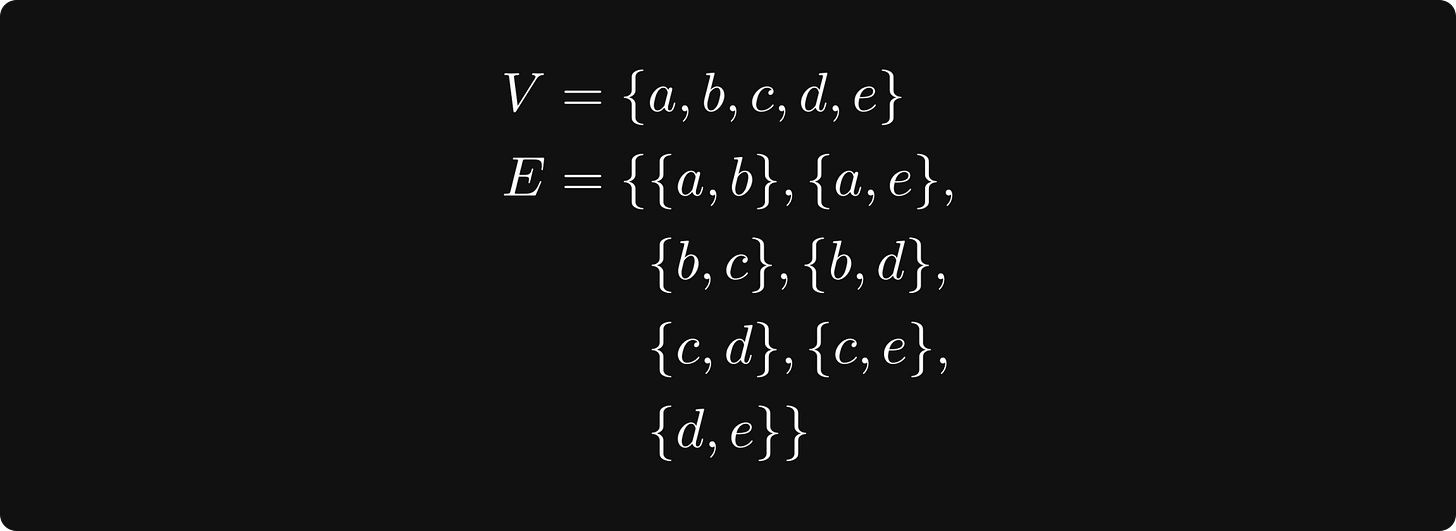Introduction to Computational Graphs

Neural Networks From Scratch lecture notes 01

Hi there!

Welcome to the second lesson of the Neural Networks from Scratch course, where we’ll build a fully functional tensor library (with automatic differentiation and all) in NumPy, while mastering the inner workings of neural networks in the process.

Last time, we looked at vectors and matrices, two of the fundamental building blocks of machine learning. (And created our custom implementations of both, serving as a backdoor Python object-oriented programming tutorial.) This time, we’ll dive deep into computational graphs, the heart of neural networks.

We’ll look at

• what graphs are,

• how to represent them in Python,

• and how to translate mathematical expressions into their language.

Let’s go!

Graphs in general

To get a grasp of computational graphs, we first take a look at plain old vanilla graphs. (Or just graphs, if you want to be academic about it.)

The main purpose of this introduction is not to dig deep into the mathematical nuances, but to get an intuitive understanding of graphs and learn how to use them in Python. Because our goal is to build neural networks, or in other words, computational graphs, we’ll use graphs extensively.

Intuitively speaking, a graph is simply a structure made of

1. nodes,

2. and edges between the nodes.

Here’s an example.

To turn the intuitive definition ”nodes and edges between them” into a mathematical one, we use sets and tuples.

Definition 1. (Graphs.) The tuple (V, E) is called a graph if V is a finite set, and E is a set of unordered pairs of V. V is called the set of nodes (or vertices), and E is called the set of edges.

This sounds a bit abstract, so let’s see an example:

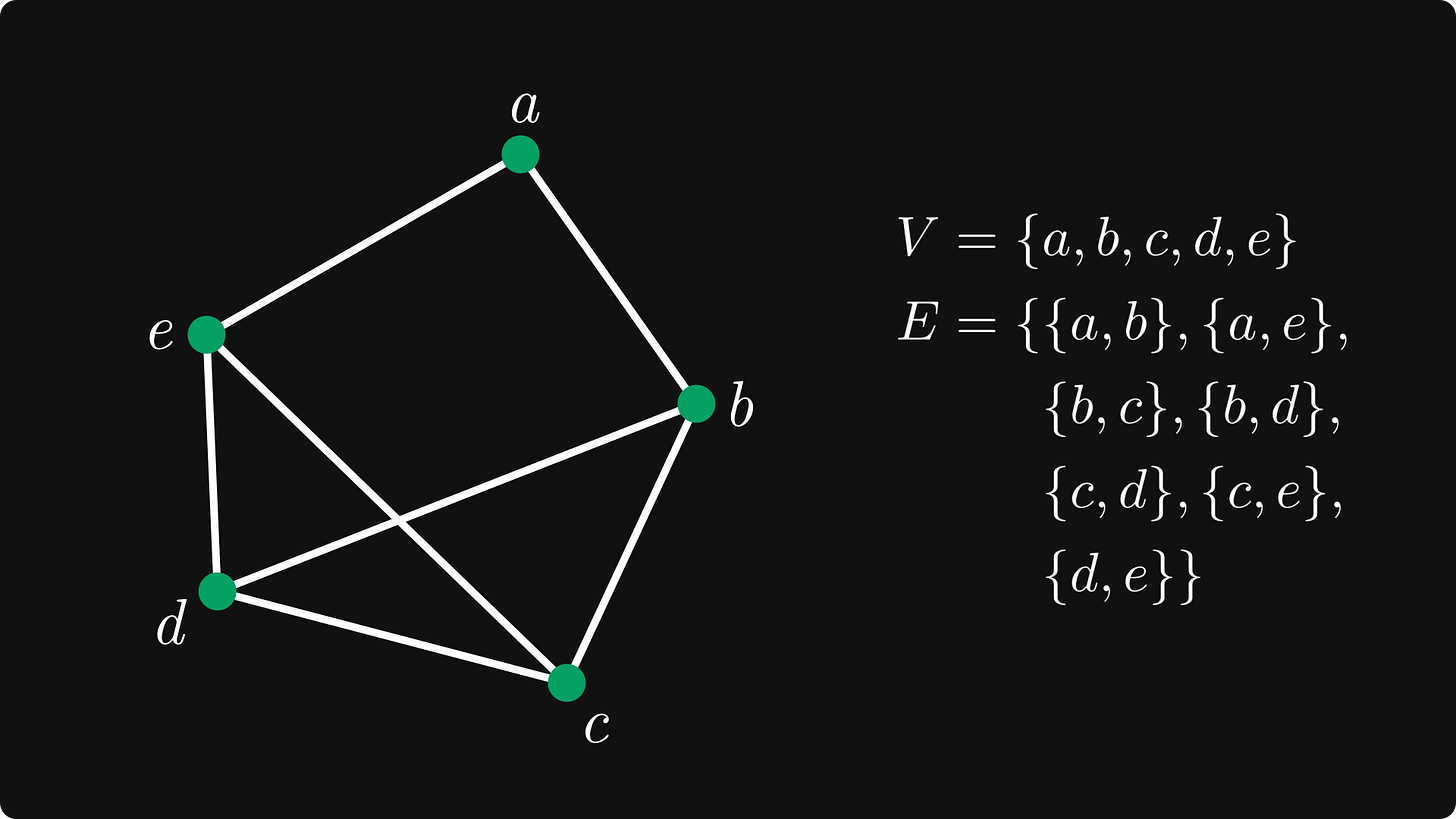
Still too abstract? Let’s draw. You won’t be surprised to see that our example graph is the one that we’ve already seen.

Let’s make the graph structure richer (and more complex). Edges can have directions, in which case, we are talking about a directed graph.

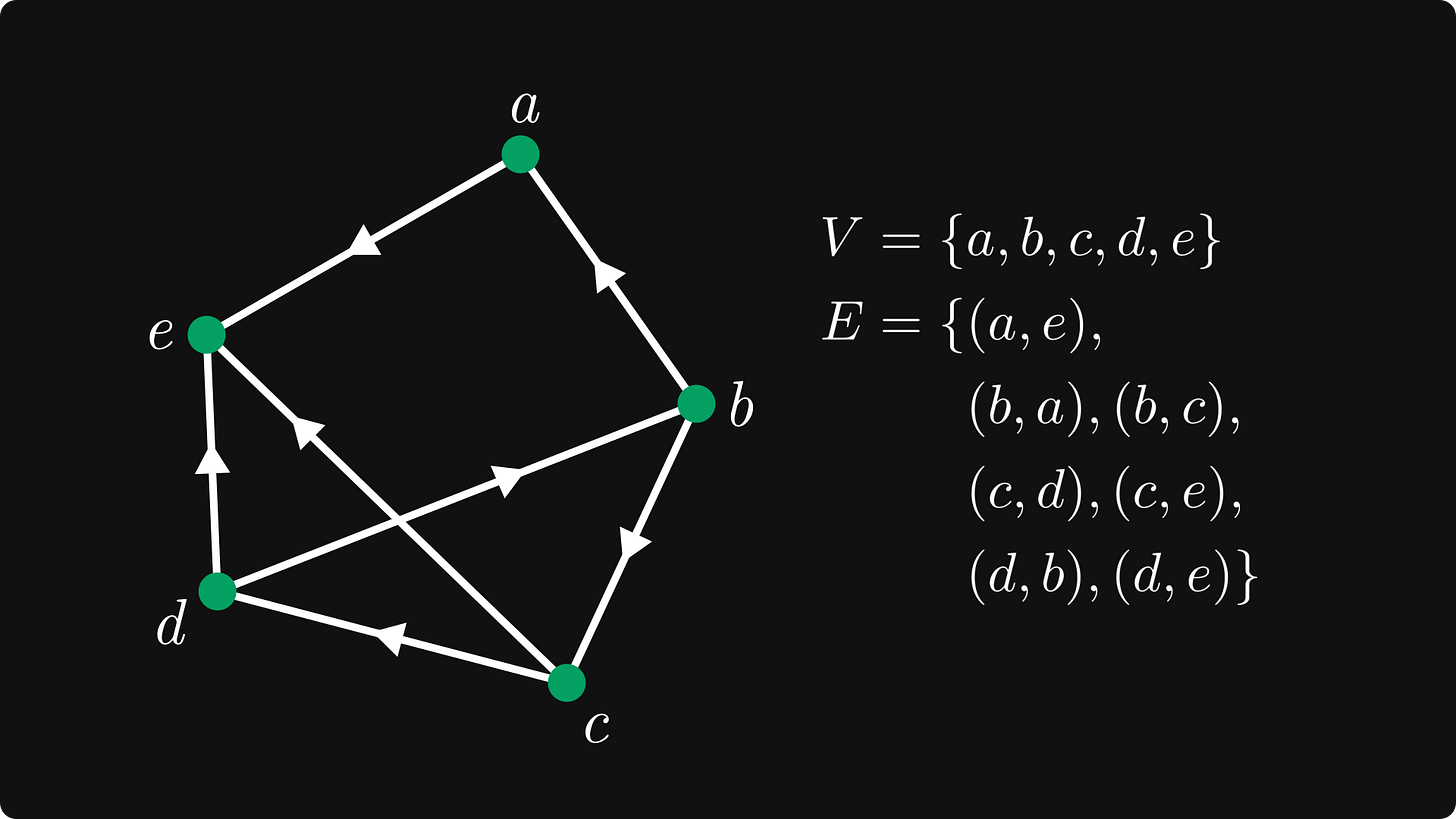
Definition 2. (Directed graphs.) The tuple (V, E) is called a graph if V is a finite set, and $ E ⊆ V × V is a set of ordered tuples of V.

Mathematically, we are still speaking about the same (V, E) structure, but this time, the edges are ordered tuples (u, v) ∈ E instead of sets. Thus, (u, v) ∈ E means an edge that starts from u and goes to v.

Check out a directed version of our example graph. We can simply visualize directed edges by putting an arrow on top of them.

Let’s add one more level of complexity: weights.

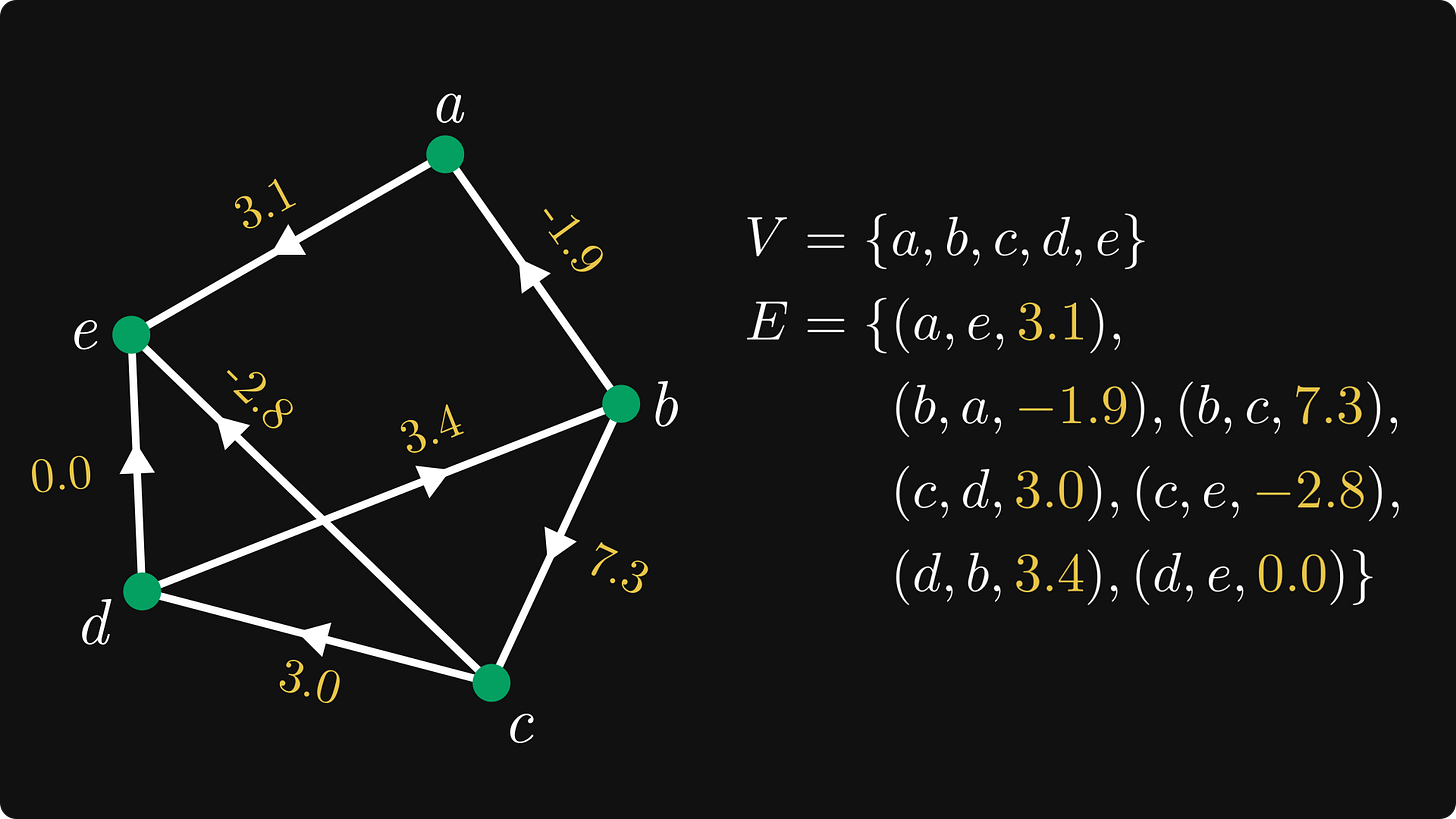
Definition 3. (Weighted and directed graphs.) The tuple (V, E) is called a weighted and directed graph if V is a finite set, and E ⊆ V × V × ℝ is a set of ordered triplets.

In English, the edges of a weighted graph consist of triplets of the form (u, v, w) ∈ V × V × ℝ, where w is called the weight.

Sounds simple enough. Now, let’s put all of this theory into practice!

You know the drill: it’s time for the implementations.