How does the Japanese multiplication work?
Discover more from The Palindrome
How does the Japanese multiplication work?
Counting sticks and stones
The Japanese multiplication method makes everybody feel "I wish they taught math like this in school."
It's not just a cute visual tool: it illuminates how and why long multiplication works.
Here is the full story.
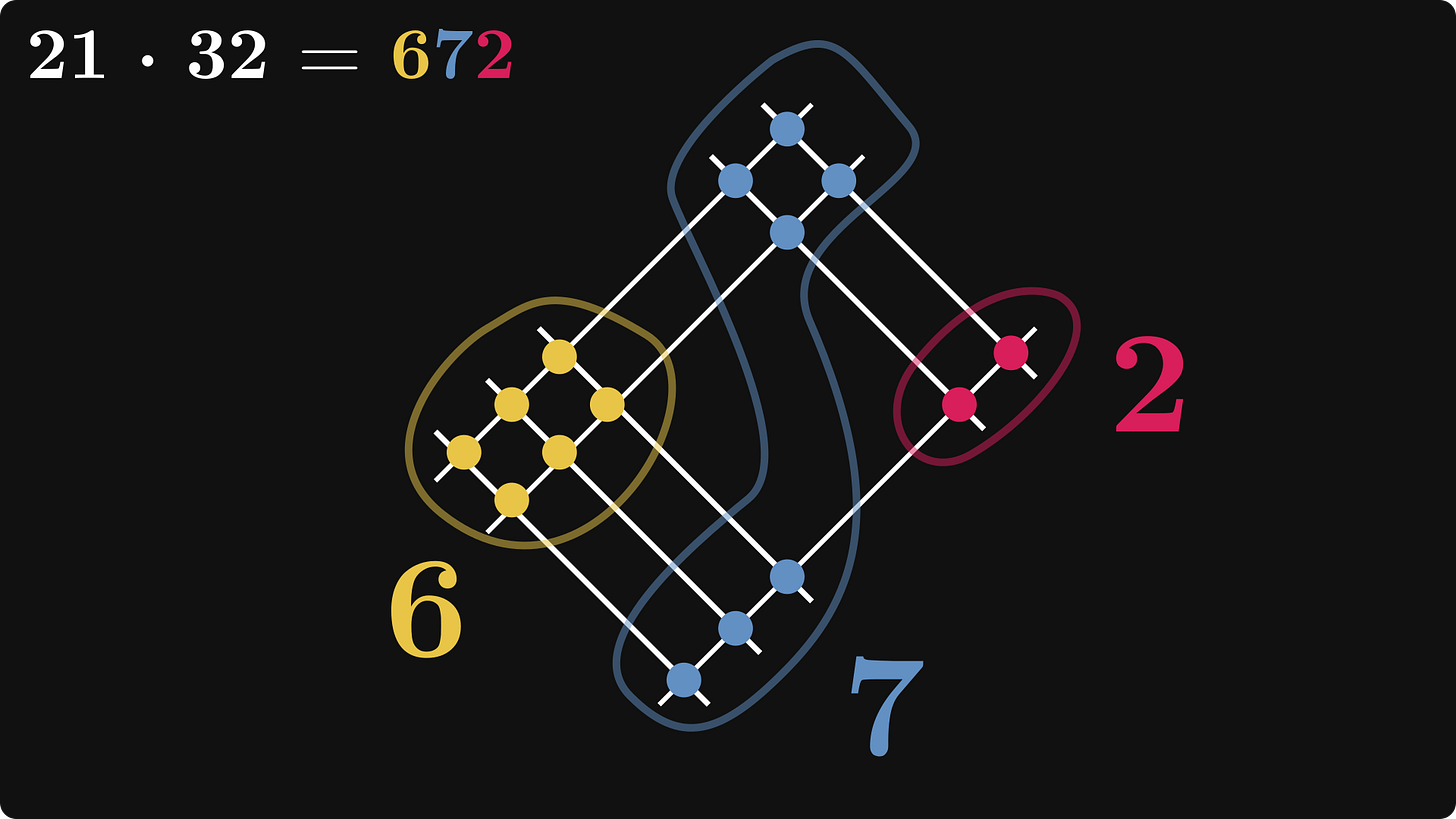
First, the Japanese multiplication method.
The first operand (21 in our case) is represented by two groups of lines: two lines in the first (1st digit), and one in the second (2nd digit).
One group for each digit.
Similarly, the second operand (32) is encoded with two groups of lines, one for each digit.
These lines are perpendicular to the previous ones.
Now comes the magic.
Count the intersections among the lines. Turns out that they correspond to the digits of the product 21 · 32.
What is this sorcery?
Let’s decompose the operands into tens and ones before multiplying them together.
By carrying out the product term by term, we are doing the same thing!
Here it is, visualized on our line representation.
There’s more. How do we multiply 21 · 32 by hand?
First, we calculate 21 · 30 = 630, then 21 · 2
= 42, which we sum up to get 21 · 32 = 672.
We learn this at elementary school like a cookbook recipe: we don’t learn the why, just the how.
Why is this relevant?
Because this is exactly what happens with the Japanese multiplication method!
Check this out one more time.
What’s the lesson here?
That visual and algebraic thinking go hand in hand. The Japanese method spectacularly illustrates how multiplication works, but with the algebra behind it, we feel the pulse of long multiplication.
We are not just mere users; we see behind the curtain now.
How does the Japanese multiplication work?
Okay, now do 75x99.
This reminds me of the time Feynman was teaching in Brazil and an abacus salesman cornered him. He could do the simple operations with simple numbers very quickly, but the harder the operation (multiplication, division, exponents, logs), the more Feynman pulled ahead. He tried to explain to the man how he did it, but the salesman couldn't follow. He just didn't understand numbers. This looks like it's doing the same thing -- setting students up neither to understand numbers in a way that aids learning more advanced operations nor to handle anything simple numbers. This is fine for the bottom 20% of the class but the rest of the class can, and needs to, take on a lot more so as not to do the sort of wheelspinning that forestalls preparedness for starting a STEM degree.